Равнобедренные треугольники – это особый класс треугольников, у которых две стороны равны друг другу. В данной статье мы рассмотрим интересное геометрическое свойство равнобедренных треугольников, связанное с биссектрисой угла, создающего равнобедренный треугольник.
Если взять равнобедренную трапецию и провести четыре биссектрисы, а затем соединить точки пересечения этих биссектрис – получится параллелограмм. Это удивительное свойство встречается временами и в других геометрических фигурах.
Метод разделения треугольника
Этот метод часто используется для доказательства равенства или равнобедренности треугольников, а также для нахождения геометрических центров и точек пересечения различных линий или отрезков внутри треугольника.
Применение метода разделения треугольника позволяет упростить геометрические рассуждения и получить более наглядные и четкие доказательства свойств треугольников и других геометрических фигур.
Описание метода и его особенности

Для доказательства разделения равнобедренного треугольника биссектрисой параллелограмма следует провести биссектрису угла равнобедренного треугольника, выходящего из вершины, которая лежит на другой стороне параллелограмма.
Особенностью данного метода является то, что биссектриса делит параллелограмм на две равные фигуры, что приводит к доказанному утверждению о разделении равнобедренного треугольника пополам.
Равнобедренный треугольник
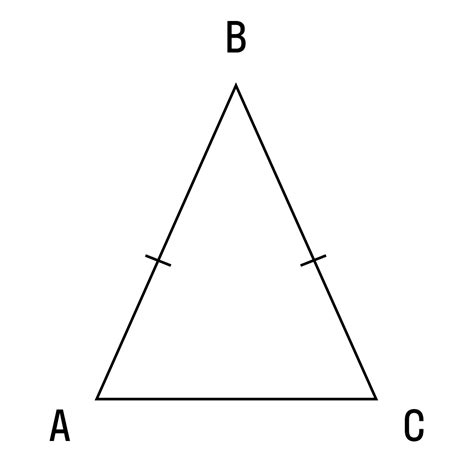
Равнобедренным треугольником называется треугольник, у которого две стороны и два угла равны. Такой треугольник обладает особыми свойствами, например, биссектриса угла, противолежащего равным сторонам, равна медиане от этой стороны. Также все высоты равнобедренного треугольника равны между собой, что делает его форму легко узнаваемой. Равнобедренные треугольники часто используются в геометрии и математике для доказательства различных теорем и утверждений.
Понятие равнобедренного треугольника

Биссектриса треугольника
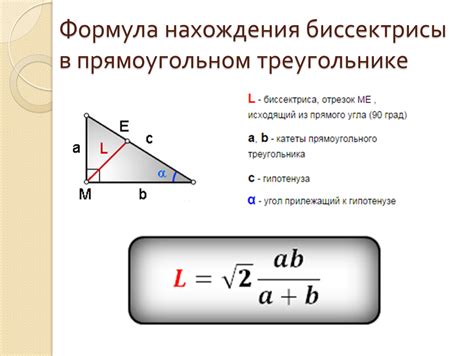
Биссектрисы в равнобедренном треугольнике равны и проходят через точку деления основания.
Свойства биссектрисы треугольника

Биссектриса пересекает сторону треугольника в точке, деля ее пропорционально двум другим сторонам.
Точка пересечения биссектрис внутреннего угла с противоположной стороной треугольника равноудалена от вершин угла.
Параллелограмм
Вопрос-ответ

Как доказать, что биссектриса угла равнобедренного треугольника делит его на два равных по площади треугольника?
Чтобы доказать это, достаточно провести биссектрису угла равнобедренного треугольника и затем рассмотреть два образовавшихся треугольника. Они будут подобны по двум сторонам и общему углу, следовательно, равны по площади.
Какой геометрический факт лежит в основе доказательства разделения равнобедренного треугольника биссектрисой?
Основной геометрический факт, на котором основано доказательство, заключается в том, что биссектриса угла равнобедренного треугольника является также медианой и высотой этого треугольника. Это позволяет доказать равенство площадей треугольников, образованных биссектрисой.
Каким образом биссектриса угла равнобедренного треугольника делит его на два равных по площади треугольника?
Биссектриса угла равнобедренного треугольника делит его на два равных по площади треугольника за счет особенностей подобия треугольников, образованных этой биcсектрисой. Эта особенность заключается в том, что два треугольника, образованные биссектрисой, подобны по двум сторонам и общему углу, что приводит к равенству их площадей.



