Поиск минимума функции является важной задачей в области оптимизации, ведь это позволяет найти наилучшее решение для задачи при заданных ограничениях. Существует множество методов поиска минимума, каждый из которых имеет свои особенности и применение в зависимости от характеристик функции и требуемой точности результата.
В данной статье мы рассмотрим несколько эффективных методов поиска минимума функции и приведем практические примеры их применения.
Использование правильного метода поиска минимума функции может значительно ускорить процесс оптимизации и повысить эффективность поиска наилучшего решения. Ознакомившись с примерами применения различных методов, вы сможете лучше понять и выбрать подходящий метод для вашей задачи.
Минимум функции: принципы и подходы
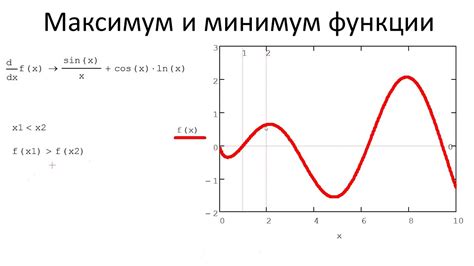
Один из основных принципов – использование градиентного спуска. Этот метод основан на поиске направления, в котором функция убывает наиболее быстро. Градиентный спуск позволяет быстро приблизиться к минимуму функции.
Другим популярным подходом является метод Ньютона. Он основан на использовании второй производной функции и позволяет найти точный минимум с меньшим количеством итераций, чем градиентный спуск.
Кроме того, существует ряд эвристических методов, таких как имитация отжига, генетические алгоритмы и роящиеся частицы. Эти методы позволяют исследовать пространство поиска минимума функции и находить оптимальные решения в сложных задачах.
Метод золотого сечения

Суть метода заключается в том, что на каждой итерации алгоритм выбирает две точки внутри заданного отрезка, таким образом, что отрезок делится в отношении золотого сечения. После этого алгоритм оценивает значения функции в этих точках, и в зависимости от результатов выбирает новый отрезок для дальнейшего исследования.
Преимущества метода золотого сечения включают его простоту и эффективность по сравнению с некоторыми другими методами оптимизации. Однако, как и любой численный метод, он имеет свои ограничения и возможные препятствия.
Градиентный спуск: основные шаги
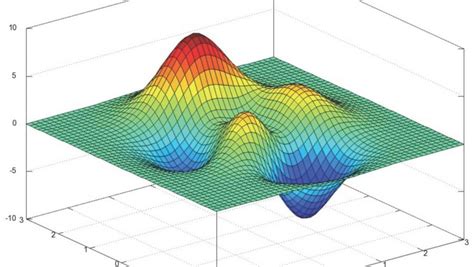
Основные шаги алгоритма градиентного спуска:
- Инициализация: задание начального приближения для минимума функции.
- Рассчитывание градиента: вычисление производной функции в текущей точке.
- Обновление параметров: изменение текущей точки в сторону, противоположную градиенту.
- Проверка условия остановки: проверка на достижение заданного критерия остановки (например, предельного количества итераций или достижение необходимой точности).
- Повторение шагов 2-4 до выполнения условия остановки.
Градиентный спуск эффективен в случае гладких функций, когда градиент хорошо определен, и может быть применен в различных областях, таких как машинное обучение, оптимизация и др.
Метод Ньютона: применение в задачах

Применение метода Ньютона возможно в различных задачах оптимизации, например, при настройке параметров моделей машинного обучения или при решении задач математического программирования. Метод Ньютона позволяет быстро сойтись к локальному минимуму функции и улучшить качество решения задачи.
- Пример задачи: минимизация функции Rosenbrock
- Пример задачи: нахождение оптимальных параметров модели линейной регрессии
- Пример задачи: оптимизация портфеля инвестиций с учетом риска и доходности
Эволюционные алгоритмы: поиск оптимального значения

Основная идея эволюционных алгоритмов заключается в использовании популяции индивидуумов для поиска оптимального значения функции.
- Эволюционные алгоритмы рассматриваются как стохастические методы оптимизации, которые оперируют с популяциями решений.
- Процесс эволюции включает в себя операции скрещивания, мутации и селекции, которые направлены на улучшение качества решений.
- Популяция в процессе эволюции постепенно приближается к оптимальному решению путем обновления и совершенствования индивидуальных хромосом.
Эволюционные алгоритмы могут быть эффективны в задачах оптимизации, где требуется поиск глобального минимума функции при наличии множества локальных оптимумов.
Алгоритм симуляции отжига: преимущества и примеры

Основные преимущества алгоритма симуляции отжига:
- Глобальный поиск: способен находить глобальный минимум функции;
- Способность избегать застревания в локальных минимумах благодаря механизму случайных скачков;
- Простота реализации и универсальность применения;
- Параметризуемость: возможность настройки параметров для оптимизации процесса.
Пример применения алгоритма симуляции отжига:
Представим задачу коммивояжёра, где необходимо найти кратчайший маршрут, проходящий через все города. Алгоритм симуляции отжига может использоваться для оптимизации маршрута и нахождения его минимальной длины.
Монте-Карло метод: случайный поиск минимума
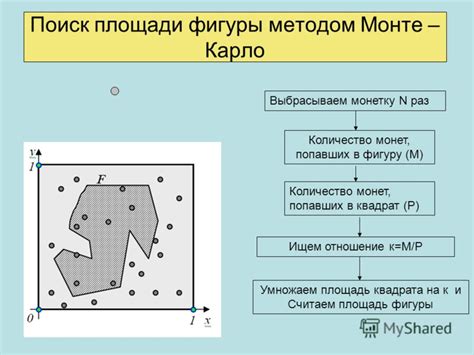
Основная идея метода заключается в проведении серии случайных экспериментов, в ходе которых выбираются точки в пространстве параметров и оценивается значение функции в этих точках.
Пусть требуется найти минимум функции f(x) на отрезке [a, b]. Монте-Карло метод заключается в генерации случайных точек x на отрезке [a, b], оценке значений функции f(x) в этих точках и выборе точки с наименьшим значением функции.
Преимущества метода заключаются в его простоте и универсальности, что позволяет применять его в широком спектре задач, однако требуется большое число итераций для достижения точного результата.
Дифференциальная эволюция: сравнение с другими методами

| Метод | Преимущества DE |
|---|---|
| Градиентный спуск | DE не требует вычисления градиента, что делает его применимым для функций, у которых градиент неизвестен или дорого рассчитать. DE хорошо работает в задачах с нелинейными и шумными функциями. |
| Метод Ньютона | DE не требует вторых производных, что делает его проще в реализации и менее подверженным ошибкам. DE имеет лучшую сходимость для сложных функций с множеством локальных минимумов. |
| Метод имитации отжига | DE обычно сходится быстрее к глобальному минимуму и имеет более высокую вероятность избегания застревания в локальных оптимумах. |
Сравнение эффективности методов поиска минимума функции

Для сравнения эффективности различных методов поиска минимума функции часто используют табличное представление результатов.
| Метод | Сложность | Скорость сходимости | Точность |
|---|---|---|---|
| Метод градиентного спуска | Средняя | Высокая | Высокая |
| Метод Ньютона | Высокая | Очень высокая | Высокая |
| Метод сопряженных градиентов | Высокая | Высокая | Высокая |
Вопрос-ответ

Какой метод поиска минимума функции является наиболее эффективным?
Наиболее эффективный метод поиска минимума функции зависит от конкретной функции, ее свойств и особенностей. Существует несколько методов, таких как метод градиентного спуска, метод Ньютона, метод Бройдена-Флетчера-Гольдфарба-Шанно (BFGS) и другие. Чаще всего эффективным оказывается комбинация различных методов и их настройка под конкретную задачу.
Можно ли найти минимум функции без градиента?
Да, можно. Существуют методы поиска минимума функции, которые не требуют наличия градиента. Например, метод случайного поиска, метод имитации отжига, метод роя частиц и другие эвристические методы. Однако, для некоторых сложных функций и задач градиентные методы обычно являются более эффективными.
Как выбрать подходящий метод оптимизации для конкретной функции?
Для выбора подходящего метода оптимизации для конкретной функции необходимо учитывать ее форму, размерность, гладкость, наличие локальных минимумов и другие характеристики. Часто для начала рекомендуется попробовать простые методы, такие как метод градиентного спуска, и затем по мере необходимости переходить к более сложным методам, в зависимости от поведения функции.
Какие практические примеры можно привести для иллюстрации методов поиска минимума функции?
Для иллюстрации методов поиска минимума функции можно рассмотреть примеры оптимизации параметров моделей машинного обучения, минимизации функций затрат в производственной деятельности, оптимизации портфеля инвестиций и т.д. Каждый из этих примеров может быть решен с использованием различных методов оптимизации, а результаты будут зависеть от выбранного подхода и настроек метода.



