Как найти медиану в равностороннем треугольнике: формула и примеры расчетов

Медиана в равностороннем треугольнике – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Этот отрезок делит сторону треугольника пополам и проходит через точку, где пересекаются медианы всех трех его сторон.

Если вам нужно найти длину медианы в равностороннем треугольнике, то для этого можно воспользоваться формулой. Длина медианы высчитывается как половина длины стороны, умноженной на коэффициент √3/2. Например, если сторона треугольника равна 10 см, то длина медианы будет равна 5√3 см.

Поиск медианы: основные понятия

Медиана равностороннего треугольника проходит через точку пересечения всех трех высот треугольника. Она также является симедианой, которая делит угол треугольника пополам и равноудалена от двух сторон.

Для расчета длины медианы в равностороннем треугольнике с помощью формулы, обычно используют свойства геометрических фигур и теоремы о центре тяжести треугольника.

Что такое медиана в треугольнике

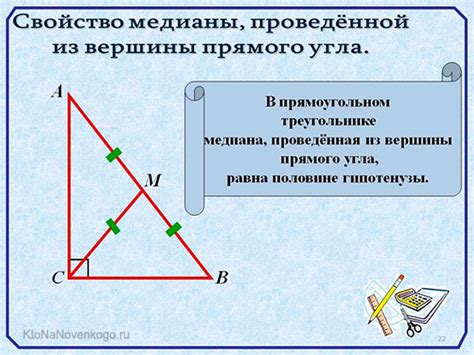
Медиана в треугольнике это отрезок, который соединяет вершину треугольника с серединой противоположной стороны.

Медианы пересекаются в точке, называемой центром тяжести или барицентром треугольника. Это точка, которая равноудалена от вершин треугольника.

Медиана делит каждую сторону треугольника пополам, и она также делит площадь треугольника пополам.

Формула для нахождения медианы

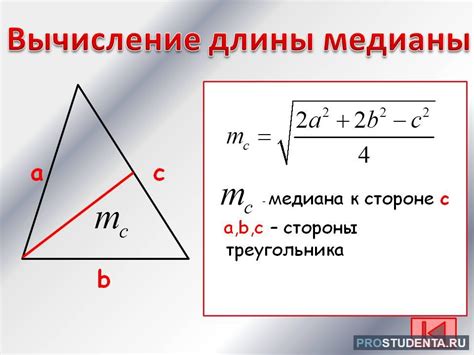
Медианы равностороннего треугольника пересекаются в одной точке, которая делит каждую медиану в соотношении 2:1. Для нахождения медианы треугольника используется следующая формула:

Медиана \(m\) равностороннего треугольника равна половине длины стороны:

\(m = \frac{1}{2}l\), где \(l\) - длина стороны треугольника.

Расчет медианы в равностороннем треугольнике

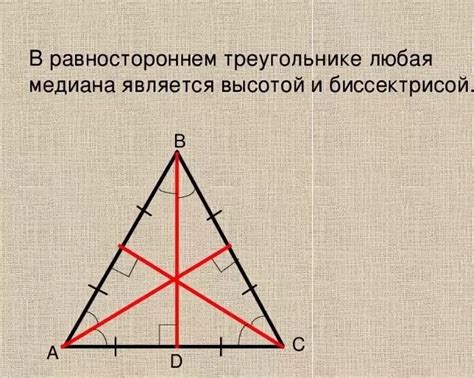
Для равностороннего треугольника формула для расчета длины медианы выглядит следующим образом:

Медиана медианы треугольника равна половине длины любой из сторон треугольника, то есть м = a / 2, где a - длина стороны треугольника.

Например, если сторона равностороннего треугольника равна 6 см, то длина медианы будет равна 3 см.

Пример нахождения медианы

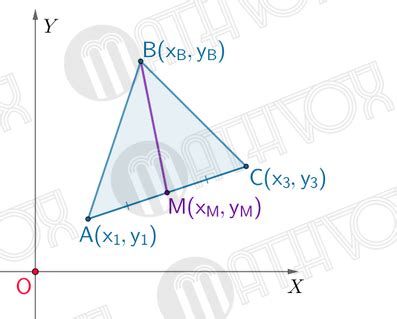
Для нахождения медианы в равностороннем треугольнике можно воспользоваться формулой: медиана равна половине длины основания треугольника. Предположим, у нас есть равносторонний треугольник со стороной основания равной 8 см.

Тогда для нахождения длины медианы мы можем взять половину длины основания:

Медиана = 1/2 * 8 = 4 см.

Таким образом, длина медианы равностороннего треугольника со стороной 8 см будет составлять 4 см.

Шаги для точной оценки

Для расчета медианы равностороннего треугольника следуйте этим шагам:

Найдите центр описанной окружности: Он совпадает с центром треугольника и пересекает все вершины.
Соедините центр с вершинами: Полученные линии являются медианами треугольника.
Измерьте длины медиан: Для вычисления медианы найдите половину длины медианы, проведенной из вершины треугольника.
Сложите найденные значения: После того как вы нашли длины всех трех медиан, сложите их вместе и поделите на 3 - получите медиану треугольника.

Вопрос-ответ