Синус и косинус – это математические функции, широко используемые в различных областях науки и техники. Они возникают в контексте изучения геометрии и тригонометрии, углубляя понимание связи между различными элементами фигур и фигурными функциями.
Синус и косинус являются отношениями сторон прямоугольного треугольника и, в то же время, представляют собой периодические функции, которые можно ассоциировать с окружностью.
В данной статье мы рассмотрим, каким образом синус и косинус связаны с окружностью, каковы их основные свойства и как можно использовать эти функции в практических задачах, включая моделирование движения, обработку сигналов и другие приложения.
Основные свойства синуса и косинуса
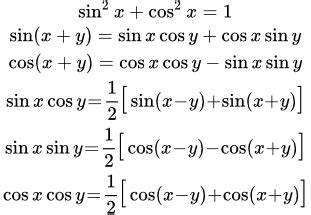
1. Синус и косинус периодичны функции с периодом \(2\pi\):
- \(\sin(x + 2\pi) = \sin(x)\)
- \(\cos(x + 2\pi) = \cos(x)\)
2. Ограниченные функции: \(|\sin(x)| \leq 1\), \(|\cos(x)| \leq 1\).
3. Значения синуса и косинуса важны на единичной окружности:
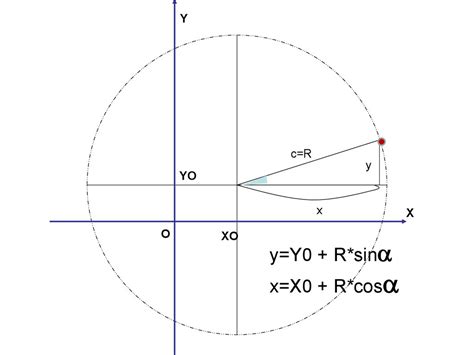
- Синус угла равен \(y\)-координате точки на окружности.
- Косинус угла равен \(x\)-координате точки на окружности.
4. Отношения между синусом и косинусом в прямоугольном треугольнике:
- \(\sin(\theta) = \frac{\text{противоположный катет}}{\text{гипотенуза}}\)
- \(\cos(\theta) = \frac{\text{прилежащий катет}}{\text{гипотенуза}}\)
Периодическая функция
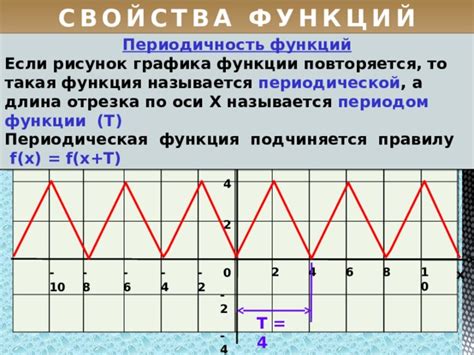
Эти функции широко используются в различных областях науки и техники для анализа периодических явлений, моделирования волн, решения математических задач и других целей.
Геометрическое представление на окружности
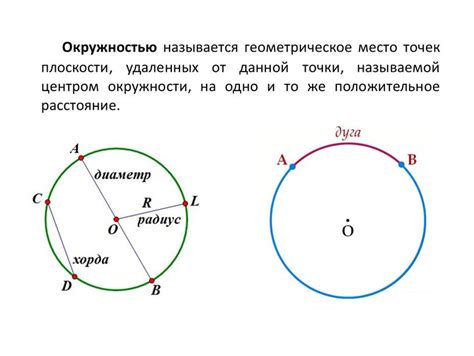
При изучении функций синуса и косинуса на окружности, геометрическое представление играет важную роль. На единичной окружности единица радиуса используются углы и длины дуг, связанные с тригонометрическими функциями.
| Угол | Синус | Косинус |
|---|---|---|
| 0° | 0 | 1 |
| 90° | 1 | 0 |
| 180° | 0 | -1 |
| 270° | -1 | 0 |
| 360° | 0 | 1 |
Этот геометрический подход помогает лучше понять связь между углами на окружности и значениями синуса и косинуса, что пригодится при решении задач и построении графиков функций.
Практическое применение синуса и косинуса
Примеры практического применения:
1. Механика и статика: Синус и косинус используются для расчета силы, напряжения, угла наклона и других параметров в механических системах.
2. Строительство и геодезия: Для определения высоты, длины сторон, углов наклона, а также в строительстве зданий и сооружений.
3. Электротехника: При анализе переменного тока, фазовых углов, колебаний в электрических цепях.
Использование синуса и косинуса позволяет точно описывать и анализировать разнообразные физические явления в различных областях инженерии и науки.
Тригонометрические и геометрические задачи

Для решения многих тригонометрических и геометрических задач полезно знать основные свойства и формулы синуса и косинуса на окружности. Например, при работе с треугольниками на плоскости часто требуется использовать соотношения между углами и сторонами. С помощью тригонометрических функций можно решать задачи на определение длины сторон, углов, площади фигур и другие геометрические задачи.
Геометрические задачи, которые можно решить с помощью тригонометрических функций включают в себя нахождение длины отрезков, площадей фигур, вычисление углов между прямыми и плоскостями, а также нахождение координат точек на плоскости.
Пример:
Дан треугольник ABC, в котором известны стороны и углы. Необходимо найти длину третьей стороны и величину оставшегося угла. С помощью тригонометрических функций синуса и косинуса можно вычислить эти значения и продолжать работу над задачей.
Таким образом, знание функций синуса и косинуса на окружности позволяет эффективно решать тригонометрические и геометрические задачи в различных областях математики и естественных наук.
Вопрос-ответ

Зачем нужно изучать функции синуса и косинуса на окружности?
Изучение функций синуса и косинуса на окружности помогает понять геометрические свойства окружности, а также найти практические применения в различных областях, например, в физике, инженерии, компьютерной графике и многих других.
Какие значения принимают синус и косинус на окружности?
Значения синуса и косинуса на окружности ограничены от -1 до 1. Синус равен высоте точки на окружности, а косинус равен основанию перпендикуляра, опущенного из этой точки.
Какую роль играют синус и косинус в тригонометрии?
Синус и косинус используются для описания отношений между сторонами и углами в прямоугольном треугольнике, для решения задач связанных с периодическими функциями и для аппроксимации сложных функций.
Каковы основные свойства функций синуса и косинуса на окружности?
Основные свойства функций синуса и косинуса на окружности включают периодичность, ограниченность значений, нечетность синуса и четность косинуса, зависимость от угла и прочие свойства, которые помогают в анализе геометрических и математических задач.
Как можно применить функции синуса и косинуса на окружности в реальной жизни?
Функции синуса и косинуса широко применяются в различных областях, таких как физика (акустические волны, колебания), инженерия (передача движения, конструкция мостов), компьютерная графика (анимация, моделирование), астрономия (расчеты орбит планет), медицина (обработка сигналов), а также в других науках и технических сферах.



