Графики функций являются важным инструментом в математике, позволяющим визуализировать зависимость между переменными. Особенно часто используются графики линейных функций, которые представляют собой прямые линии на плоскости. Понимание процесса построения графика линейной функции отражает глубокое понимание самой функции и ее свойств.
Построение графика линейной функции не является сложной задачей, если следовать определенному алгоритму. В данном руководстве мы шаг за шагом рассмотрим процесс построения графика линейной функции, начиная с определения уравнения прямой и заканчивая построением самого графика с помощью метода координатных осей.
Понимание построения графика линейной функции поможет не только визуализировать зависимость между переменными, но и решать множество задач по анализу данных, прогнозированию и моделированию различных явлений.
Построение графика линейной функции
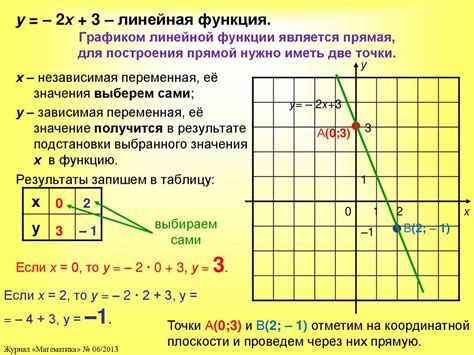
Сначала определяем координаты точек, через которые будет проходить прямая. Для этого выбираем две удобные точки, подставляем их координаты в уравнение и находим значения y.
После определения точек строим оси координат. Прямая проходит через точки (0, b) и (1, k + b), где b – значение b коэффициента, k – значение k коэффициента.
Используем найденные точки для отметки на графике и проводим прямую через них. График линейной функции будет представлен в виде прямой линии на графике.
Определение основных понятий

Перед тем как начать строить график линейной функции, важно определить основные понятия, которые понадобятся в процессе работы. Основные понятия включают в себя:
1. Линейная функция - математическая функция, описываемая уравнением вида y = mx + b, где m - коэффициент наклона, b - коэффициент сдвига.
2. Система координат - графическое представление функции на плоскости с использованием осей x и y.
3. Угловой коэффициент - коэффициент m в уравнении линейной функции, который определяет наклон прямой.
4. Точка пересечения с осью y - точка, в которой линейная функция пересекает ось y и имеет координату (0, b).
Понимание этих основных понятий поможет вам более эффективно построить график линейной функции.
Шаг 1: Нахождение углового коэффициента
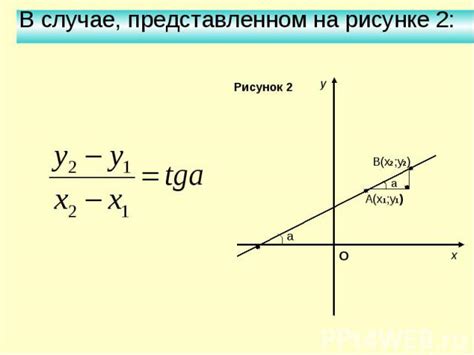
Чтобы построить график линейной функции, сначала необходимо найти угловой коэффициент этой функции. Угловой коэффициент (k) определяется как коэффициент перед переменной x в уравнении функции f(x) = kx + b.
Для нахождения углового коэффициента можно использовать следующий метод:
| 1. Выберите две точки на графике функции, которые легко считать |
| 2. Найдите изменение значения функции (Δy) и изменение значения аргумента (Δx) между этими двумя точками |
| 3. Угловой коэффициент вычисляется как отношение Δy к Δx: k = Δy / Δx |
После того, как угловой коэффициент найден, можно перейти к следующему шагу построения графика линейной функции.
Шаг 2: Нахождение координат точек
Чтобы построить график линейной функции, нужно определить несколько точек на оси координат. Для этого подставьте различные значения переменной x в уравнение функции и найдите соответствующие значения y.
Шаги по нахождению координат точек:
- Выберите несколько значений переменной x, например, -2, 0, 2.
- Подставьте эти значения в уравнение функции y = kx + b и найдите соответствующие значения y.
- Запишите полученные координаты точек (x, y).
После того, как найдены несколько точек, можно построить график, соединив их линией. Это поможет визуализировать линейную функцию и легче понять её свойства.
Вопрос-ответ

Как определить коэффициенты k и b в уравнении линейной функции?
Коэффициент k (наклон) определяется по формуле k = (y2 - y1) / (x2 - x1), где (x1, y1) и (x2, y2) - координаты двух точек на прямой. Коэффициент b (смещение) равен y-интерсепту, т.е. значение y при x = 0.
Что делать, если функция не задана в виде y = kx + b?
Если функция не задана в виде y = kx + b, а в другом виде, нужно привести ее к этому виду, выделив коэффициенты k и b. Например, если функция задана в виде y = mx + c, где m - коэффициент наклона, а c - свободный член, то k = m и b = c.



