Основной символ импликации – стрелка "→". Выражение "A → B" означает, что если утверждение A истинно, то и утверждение B также является истинным. Если же утверждение A ложно, то из этого ничего не следует о истинности или ложности утверждения B. В логике импликация обычно определена как соотношение истинности между двумя утверждениями без участия логических операций.
Для понимания импликации важно уметь выделять предпосылки и следствия в рассматриваемых утверждениях, а также учитывать контекст, в котором они используются. Для иллюстрации данного понятия можно привести примеры из математики, философии или реальной жизни, где принцип импликации играет решающую роль в построении аргументов и доказательств.
Основной принцип импликации

Основной принцип импликации заключается в том, что если утверждение A влечет за собой утверждение B, то из истинности утверждения A следует истинность утверждения B. Иными словами, если A => B, то из A следует B.
Этот принцип важен в логике и рассматривается как одно из основных свойств отношения импликации. Он используется для определения логической связи между утверждениями и для построения логических рассуждений.
Структура условного высказывания

Условное высказывание в логике имеет следующую структуру:
- Предпосылка (условие): это предложение, от которого зависит истинность или ложность основного утверждения.
- Основное утверждение: это высказывание, которое зависит от выполнения условия.
- Связующее слово: слово или фраза, которые связывают предпосылку и основное утверждение, указывая на зависимость между ними.
Пример условного высказывания: "Если сегодня идет дождь, то улицы будут мокрыми".
- Предпосылка: "сегодня идет дождь".
- Основное утверждение: "улицы будут мокрыми".
- Связующее слово: "если...то...".
Примеры импликации
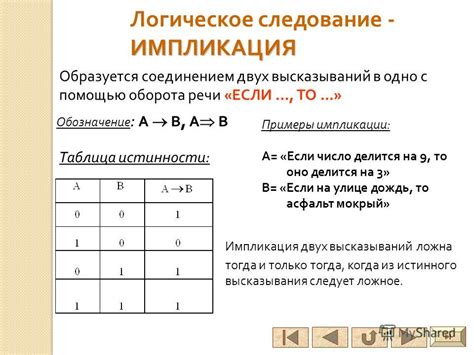
Импликация играет важную роль в логике и математике. Рассмотрим несколько примеров, чтобы лучше понять этот логический концепт:
| Утверждение P | Утверждение Q | Импликация (P → Q) |
| Сегодня понедельник | Завтра вторник | Если сегодня понедельник, то завтра вторник |
| Россия - страна Европы | Москва - столица России | Если Россия - страна Европы, то Москва - столица России |
| Человек родился в США | Он говорит по-английски | Если человек родился в США, то он говорит по-английски |
Импликация в повседневной жизни

Импликация, как логический принцип, часто применяется не только в математике или философии, но и в повседневной жизни. Как пример, можно рассмотреть обыденные ситуации, где выдвигается предположение и следует логическое заключение.
Например, если вы видите, что облака сгущаются и темнеют, можно сделать импликацию: "Скоро пойдет дождь". Это основано на логическом связывании между фактом возрастания темноты облаков и прогнозом дождя.
Вопрос-ответ

Что такое импликация в логике?
Импликация - это логическая связь между двумя утверждениями, при которой одно утверждение (посылка) влечет за собой другое (следствие). Если посылка истинна, то и следствие тоже истинно, иначе импликация является ложной.
Каковы основные правила импликации в логике?
Основные правила импликации в логике: импликация истинна, когда посылка и следствие истинны или когда посылка ложна; импликация ложна, когда посылка истинна, а следствие ложно.
Можете привести пример логической импликации?
Например, утверждение: "Если дождь идет, то улица мокра". В этом случае, дождь - посылка, улица мокра - следствие. Если идет дождь, то улица действительно мокра, что подтверждает импликацию.
Как определить ложность импликации в логике?
Импликация ложна в случае, когда посылка истинна, а следствие ложно. То есть, если из посылки не следует указанное следствие, импликация считается ложной.
Какую роль играет импликация в математике?
В математике импликация используется для формализации логических утверждений и построения доказательств. Она позволяет устанавливать логические связи между утверждениями и выявлять закономерности.



