Решение уравнений – важный аспект математики, который часто вызывает затруднения у учеников и студентов. Поиск корней уравнения – процесс, который требует определенных навыков и методов. В этой статье мы рассмотрим пошаговую инструкцию по нахождению корня уравнения и разберем основные шаги этого процесса.
Шаг 1: Первым шагом в решении уравнения является определение его типа – это может быть линейное, квадратное, показательное и т.д. В зависимости от типа уравнения выбирается соответствующий метод решения.
Шаг 2: Далее необходимо привести уравнение к стандартному виду, чтобы удобнее было проводить дальнейшие вычисления. Это может включать в себя выделение корней, приведение подобных слагаемых и т.п.
Выбор уравнения для решения

Прежде чем приступить к поиску корня уравнения, необходимо выбрать правильное уравнение для решения. Важно определить тип уравнения: линейное, квадратное, степенное или трансцендентное. Для каждого типа уравнения есть свои методы решения, поэтому важно определить, с каким типом уравнения вы имеете дело.
При выборе уравнения также обратите внимание на его форму и структуру. Иногда уравнение можно преобразовать к более удобной форме (сокращение, домножение, замена переменных и т.д.), чтобы упростить процесс решения.
Если у вас возникают сомнения при выборе уравнения, обратитесь к учебнику или к онлайн-ресурсам для более подробной информации о типах уравнений и методах их решения.
Определение вида уравнения

Перед тем как начинать поиск корня уравнения, необходимо определить его вид. Уравнения могут быть линейными, квадратными, кубическими и так далее. Чтобы определить вид уравнения, необходимо обратить внимание на степень неизвестной переменной.
Линейное уравнение имеет вид a*x + b = 0, где a и b - известные коэффициенты, а x - неизвестная переменная. Квадратное уравнение имеет вид a*x^2 + b*x + c = 0, где a, b и c - известные коэффициенты, а x - неизвестная переменная в квадрате.
Исследуйте уравнение, чтобы понять его вид и затем выберите подходящий метод для нахождения корня.
Преобразование уравнения
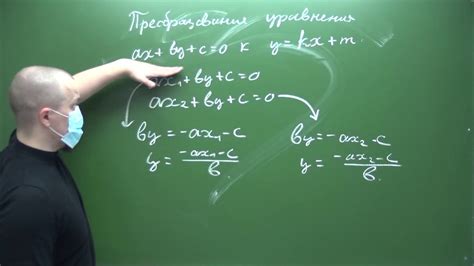
Для поиска корня уравнения обычно необходимо предварительно преобразовать его в более удобную форму.
Один из шагов преобразования может быть сведение уравнения к виду, где слева стоит 0. Для этого можно вынести все слагаемые на одну сторону уравнения, чтобы получить уравнение вида f(x) = 0.
Также необходимо убедиться, что уравнение не имеет нулевого делителя и его корень существует.
Использование свойств уравнения

Для того чтобы найти корень уравнения, необходимо использовать свойства, которые описывают его характеристики. Основные свойства уравнения включают в себя коэффициенты при переменных и свободный член. Коэффициенты перед переменными позволяют определить степень уравнения и влияют на его решение. Свободный член представляет собой значение, которое уравнение принимает при отсутствии переменных. Исходя из этих свойств, можно приступить к нахождению корня уравнения с помощью математических методов и алгоритмов.
| Свойство | Описание |
|---|---|
| Коэффициенты переменных | Определяют степень уравнения и влияют на его решение при нахождении корня. |
| Свободный член | Представляет значение уравнения при отсутствии переменных и влияет на его общую форму. |
Деление уравнения на части

Разбиение уравнения на простые выражения

Пример:
| Уравнение: | 2x^2 + 5x - 3 = 0 |
| Разбиение на простые выражения: | (2x - 1)(x + 3) = 0 |
После разбиения уравнения на простые выражения можно продолжить процесс поиска корня, используя различные методики решения уравнений. Этот шаг поможет вам систематизировать информацию и легче решить уравнение.
Поиск корня уравнения
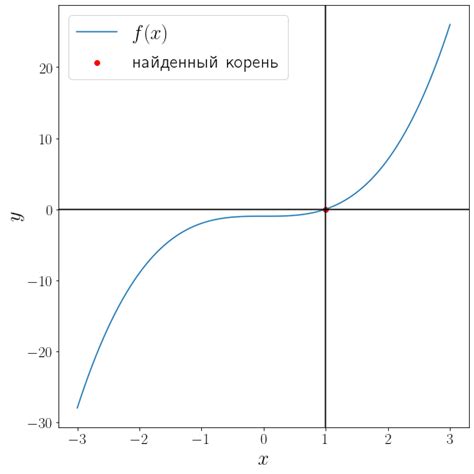
Для того чтобы найти корень уравнения, нужно использовать различные методы решения, в зависимости от типа уравнения. Представляем таблицу с основными методами поиска корня уравнения:
| Тип уравнения | Метод решения |
|---|---|
| Линейное уравнение (вида ax+b=0) | Используется метод подстановки или метод преобразования уравнения |
| Квадратное уравнение (вида ax^2+bx+c=0) | Применяются формулы дискриминанта или метод полного квадрата |
| Система уравнений | Можно использовать метод сложения или вычитания уравнений |
Зная тип уравнения и соответствующий метод решения, можно найти корень уравнения с помощью математических операций и соблюдая правила преобразования уравнений.
Вопрос-ответ

Как найти корень уравнения с помощью метода подбора?
Для того чтобы найти корень уравнения с помощью метода подбора, нужно подставлять различные значения вместо переменной и проверять, когда уравнение станет равным нулю. Например, для уравнения x^2 - 5x + 6 = 0 можно начать с подбора x=1, x=2 и так далее, пока не найдется значение переменной, при котором уравнение выполняется.
Как найти корень уравнения с помощью метода дискриминанта?
Для нахождения корней уравнения с помощью дискриминанта, нужно вычислить значение дискриминанта по формуле D = b^2 - 4ac, где уравнение имеет вид ax^2 + bx + c = 0. Затем, если D > 0, то уравнение имеет два различных действительных корня, если D = 0, то уравнение имеет один действительный корень, а если D < 0, то уравнение имеет два комплексных корня. Таким образом, метод дискриминанта позволяет определить число и тип корней уравнения.



