Точка пересечения биссектрис треугольника, также известная как центр окружности, вписанной в данный треугольник, является одной из ключевых точек в геометрии. Она обладает рядом удивительных свойств, которые позволяют использовать ее для решения различных задач.
Одно из основных свойств этой точки заключается в том, что она равноудалена от сторон треугольника. Таким образом, она является центром окружности, вписанной в данный треугольник, что позволяет использовать данное свойство для нахождения ее координат.
Кроме того, точка пересечения биссектрис треугольника также является точкой пересечения медиан и высот данного треугольника. Это позволяет использовать ее для нахождения центра тяжести треугольника и других важных точек, связанных с ним.
Роль точки пересечения биссектрис

Точка пересечения биссектрис треугольника играет важную роль в геометрии. Эта точка называется центром вписанной окружности и обладает рядом уникальных свойств.
Во-первых, центр вписанной окружности равноудален от всех сторон треугольника, что делает его центром равностороннего треугольника.
Во-вторых, сумма расстояний от центра вписанной окружности до сторон треугольника равна периметру треугольника. Это свойство имеет важное значение в задачах поиска периметра треугольника.
Таким образом, точка пересечения биссектрис треугольника является ключевой точкой, которая помогает понять геометрические свойства и взаимосвязи внутри фигуры.
Определение свойства точки пересечения биссектрис треугольника
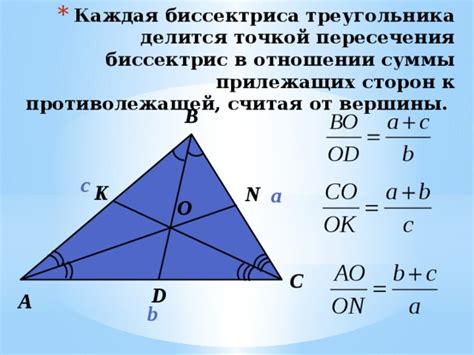
Точка пересечения биссектрис треугольника (центр вписанной окружности) равноудалена от всех сторон треугольника.
Свойство: Расстояние от точки пересечения биссектрис до каждой стороны треугольника одинаково.
Связь со сторонами треугольника
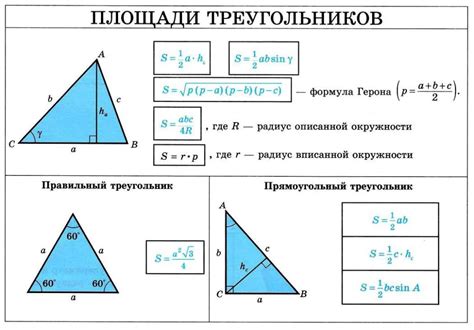
Точка пересечения биссектрис треугольника служит критической точкой, которая играет важную роль в отношении сторон треугольника. Эта точка равноудалена от сторон треугольника и делит каждую биссектрису в отношении, обратном соотношению соответствующих сторон треугольника. Таким образом, свойства точки пересечения биссектрис напрямую связаны с длинами сторон треугольника, что делает ее значимой для изучения и понимания геометрии треугольников.
Положение точки пересечения
Если треугольник остроугольный, центр вписанной окружности лежит внутри треугольника. Для тупоугольного треугольника центр вписанной окружности располагается вне треугольника. В случае прямоугольного треугольника центр вписанной окружности совпадает с вершиной прямого угла.
Геометрическое представление
Вопрос-ответ

Зачем нужны биссектрисы треугольника?
Биссектрисы треугольника - это линии, которые делят углы треугольника пополам. Точка их пересечения называется центром вписанной окружности. Биссектрисы помогают определить точку пересечения высот треугольника, а также разделить его на равные части. Также они играют важную роль в задачах геометрии, связанных с треугольниками.
Какая связь между точкой пересечения биссектрис и центром вписанной окружности?
Точка пересечения биссектрис треугольника является центром вписанной окружности в этот треугольник. Это означает, что если провести вписанную окружность в треугольник, то ее центр будет лежать в точке пересечения биссектрис. Это свойство помогает при решении задач, связанных с окружностями, вписанными в треугольники.
Как определить точку пересечения биссектрис треугольника?
Для определения точки пересечения биссектрис треугольника нужно провести биссектрисы углов треугольника. Точка их пересечения будет являться центром вписанной окружности в треугольник. Это можно сделать с помощью инструментов геометрии, таких как линейка и угольник, или с использованием геометрических программ.



