Тригонометрические функции играют важную роль в математике и естественных науках. Одним из ключевых понятий, связанных с тригонометрией, является период функции. Период – это такое число, при котором значение функции начинает повторяться, обладая определенной периодичностью.
Найти период тригонометрической функции можно с помощью различных методов и свойств. Знание периода функции позволяет правильно интерпретировать ее график и проводить дальнейшие математические операции.
В данной статье мы рассмотрим примеры решения задач по поиску периода тригонометрических функций, испытав на практике методы, которые помогут нам определить период функции и успешно применить их в математических расчетах.
Поиск периода функции: формула и методы

Для нахождения периода тригонометрической функции необходимо анализировать периодичность функции. Общая формула для периода функции sin или cos имеет вид:
Период = 2π/|b|, где b - коэффициент при x в функции.
Для функций типа y = a*sin(bx + c) или y = a*cos(bx + c) период равен 2π/|b|.
Также можно использовать метод исследования графика функции, определение точек повторяемости, или анализ периодичности через график синусоиды или косинусоиды. Корректно определенный период поможет понять поведение функции и проанализировать ее особенности.
Определение периода тригонометрической функции
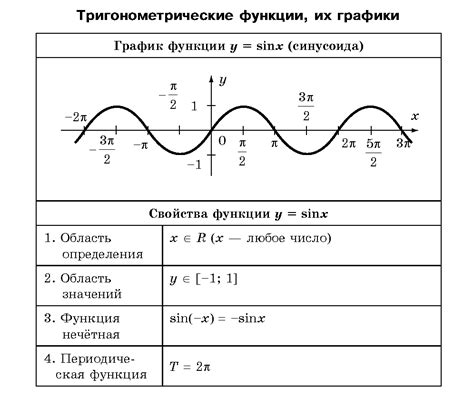
Пример решения: нахождение периода синусоиды

Для нахождения периода синусоиды следует обратить внимание на формулу периода такой функции. Для синусоиды период выражается как:
Период = 2π / k,
где k - коэффициент при переменной внутри синуса (обычно это число перед x). Например, если дано уравнение:
y = sin(3x),
то период можно найти как:
Период = 2π / 3 = 2π/3.
Таким образом, период синусоиды y = sin(3x) равен 2π/3.
Практические примеры: решение задач по поиску периода

Пример 1:
- Дана функция \( y = \cos(2x) \). Известно, что период косинуса равен \( 2\pi \), следовательно, чтобы найти период функции \( y = \cos(2x) \), нужно разделить период обычного косинуса на коэффициент перед переменной \( x \).
- Таким образом, период функции \( y = \cos(2x) \) равен \( \frac{2\pi}{2} = \pi \).
Пример 2:
- Рассмотрим функцию \( y = \sin\left(\frac{x}{3} ight) \). Период синуса равен \( 2\pi \), а здесь коэффициент перед переменной \( x \) равен \( \frac{1}{3} \).
- Следовательно, период функции \( y = \sin\left(\frac{x}{3} ight) \) равен \( 2\pi \cdot 3 = 6\pi \).
Вопрос-ответ

Как найти период тригонометрической функции?
Для поиска периода тригонометрической функции необходимо выразить функцию в виде f(x) = A*sin(Bx + C) или f(x) = A*cos(Bx + C), где A, B и C - константы. Затем период функции равен 2π/B.
Как найти период функции y = cos(3x) + sin(2x)?
Первым шагом выразим функцию y = cos(3x) + sin(2x) в виде y = A*cos(Bx + C) + D*sin(Ex + F). Нарисуем график функции и найдем, через сколько угловых градусов функция начинает повторяться. В данном случае период будет равен 2π/2 = π, так как угловые коэффициенты 3 и 2 делятся на 2 без остатка.
Как найти период функции y = 2sin(4x) - 3cos(2x)?
Преобразуем функцию y = 2sin(4x) - 3cos(2x) к виду y = A*sin(Bx + C) + D*cos(Ex + F). Для функции y = Asin(Bx) + Ccos(Dx) период равен 2π/|B|, где |B| - модуль коэффициента при x. В данном случае, у первого слагаемого B = 4, а у второго D = 2. Таким образом, период функции равен 2π/4 = π/2.



