Тригонометрия – раздел математики, изучающий связь между углами и сторонами треугольников. Углы 120 и 60 градусов являются часто встречающимися в математике и имеют особенности, которые полезно знать при работе с ними.
Угол 120 градусов равен 2/3 полного оборота и является одним из основных углов в тригонометрии. Его тригонометрические значения связаны с углом 60 градусов, который также играет важную роль в математике.
Косинус угла 120 градусов равен -1/2, а синус -√3/2. Косинус и синус угла 60 градусов связаны с косинусом и синусом угла 120 градусов специальной формулой, что делает эти углы важными при решении задач по тригонометрии.
Тригонометрические значения углов 120 и 60 градусов
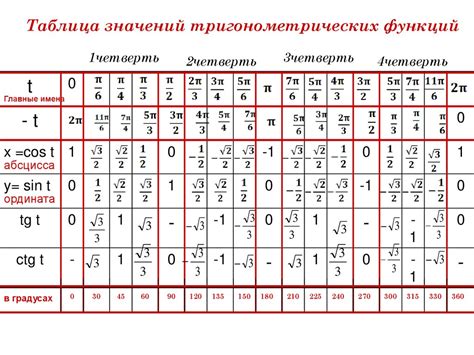
Для угла 120 градусов косинус –1/2, синус √3/2, тангенс –√3.
Для угла 60 градусов косинус 1/2, синус √3/2, тангенс √3.
Связь между углами 120 и 60 градусов
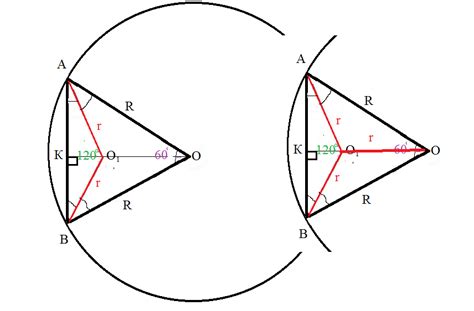
Угол 120 градусов: sin(120°) = sin(180° - 60°) = sin(60°) = √3/2
Угол 60 градусов: sin(60°) = sin(180° - 120°) = sin(120°) = √3/2
Тригонометрические функции угла 120 градусов
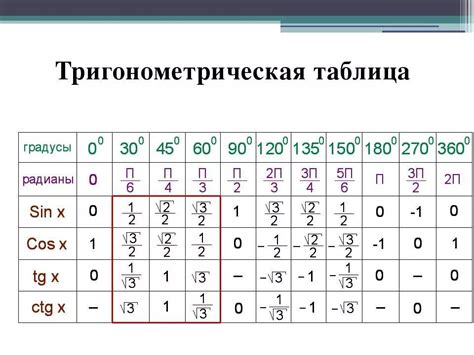
- Синус 120 градусов:
- Косинус 120 градусов:
- Тангенс 120 градусов:
- Котангенс 120 градусов:
- Секанс 120 градусов:
- Косеканс 120 градусов:
Особенности тригонометрических значений угла 120 градусов
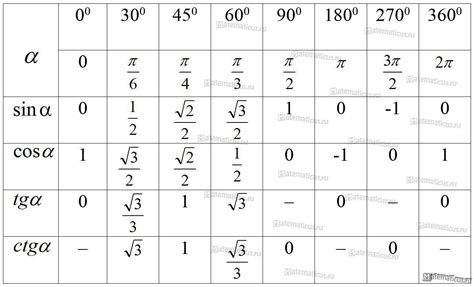
Тригонометрические значения угла 120 градусов можно легко найти, используя связь между углами 120 и 60 градусов. С помощью тригонометрических функций можно определить значения синуса, косинуса и тангенса этого угла.
- Синус угла 120 градусов равен √3/2
- Косинус угла 120 градусов равен -1/2
- Тангенс угла 120 градусов равен -√3
Эти значения отражают характеристики угла 120 градусов и его положение на координатной плоскости. Изучение особенностей тригонометрических значений поможет лучше понять связь между углами и их тригонометрическими функциями.
Тригонометрические функции угла 60 градусов
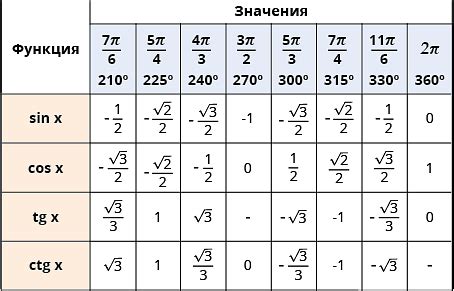
Косинус угла 60 градусов равен 0.5, что можно представить как $\cos 60^\circ = \frac{1}{2}$.
Синус угла 60 градусов также равен 0.5, то есть $\sin 60^\circ = \frac{\sqrt{3}}{2}$.
Тангенс угла 60 градусов равен $\sqrt{3}$, что можно записать как $\tan 60^\circ = \sqrt{3}$.
Касательная угла 60 градусов равна $\sqrt{3}$, т.е. $\cot 60^\circ = \frac{1}{\sqrt{3}}$.
Секанс угла 60 градусов равен 2, что выражается как $\sec 60^\circ = 2$.
Косеканс угла 60 градусов также равен 2, т.е. $\csc 60^\circ = 2$.
Особенности тригонометрических значений угла 60 градусов
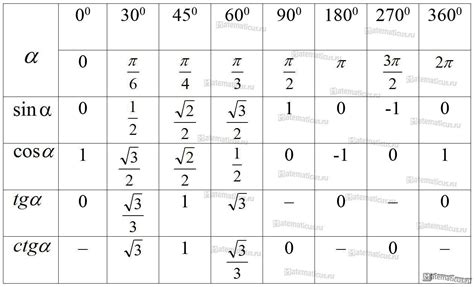
Для угла 60 градусов справедливы следующие тригонометрические значения:
Синус: sin(60°) = √3/2
Косинус: cos(60°) = 1/2
Тангенс: tg(60°) = √3
Таким образом, угол 60 градусов имеет особенно простые и характерные тригонометрические значения, что упрощает его вычисления и применение в различных задачах.
Сводная информация по значениям углов 120 и 60 градусов
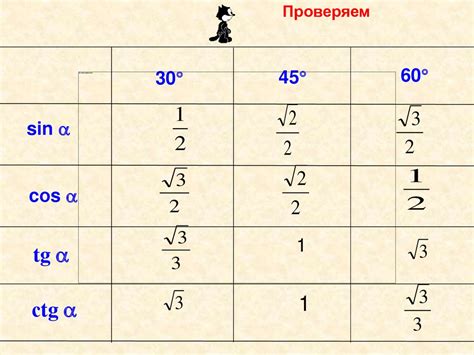
Для угла 120 градусов:
- Синус: √3/2
- Косинус: -1/2
- Тангенс: -√3
- Котангенс: -1/√3
Для угла 60 градусов:
- Синус: √3/2
- Косинус: 1/2
- Тангенс: √3
- Котангенс: 1/√3
Вопрос-ответ




