Решение системы уравнений является одной из основных задач в математике и физике. При решении системы уравнений 3x + 2y = 4, x² + 2z³ = 3 используются различные методы и приемы, которые позволяют найти значения неизвестных переменных. Это позволяет выявить точное решение системы и понять, как взаимосвязаны данные уравнения.
В данной статье рассмотрим различные методы решения системы уравнений, включая метод замены переменных, метод Гаусса, метод Крамера и другие. Каждый из этих методов имеет свои особенности и применяется в зависимости от сложности системы уравнений и предпочтений математика.
Методы решения системы уравнений

Существует несколько методов, которые помогают решить системы уравнений:
1. Метод подстановки: предполагает выражение одной переменной через другую и последующую подстановку этого выражения в другое уравнение системы.
2. Метод сложения уравнений: предполагает сложение или вычитание уравнений системы таким образом, чтобы избавиться от одной из переменных.
3. Метод Крамера: использует правило Крамера для нахождения решения системы линейных уравнений по определителям матрицы коэффициентов и матрицы свободных членов.
4. Метод Гаусса: позволяет свести систему уравнений к ступенчатому виду с последующим обратным ходом для нахождения решения.
Выбор метода зависит от сложности системы уравнений, наличия конкретных условий и предпочтений решателя.
Метод подстановки и исключения

Например, исходная система уравнений:
| 3x + 2y = 4 |
| x² + 2z³ = 3 |
Мы можем выразить переменную x через y с помощью первого уравнения (x = (4 - 2y) / 3) и подставить это выражение во второе уравнение для определения значений y и z. Далее решаем полученное уравнение и находим значения переменных.
Метод графического решения
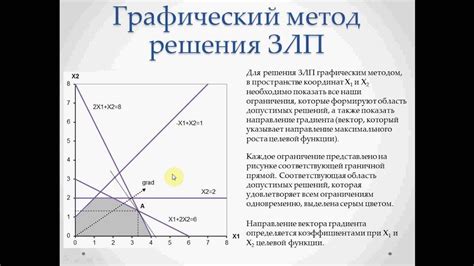
Метод матриц и определителей

Для решения системы уравнений с помощью метода матриц и определителей необходимо представить уравнения в матричной форме.
Запишем систему уравнений в виде расширенной матрицы:
| 3 | 2 | 0 | | | 4 |
| 1 | 0 | 2 | | | 3 |
Далее вычисляем определитель основной матрицы и определители матриц, полученных заменой столбца свободных членов соответственно коэффициентам переменных.
Если определитель основной матрицы не равен нулю, система совместна и имеет единственное решение.
В противном случае, система либо несовместна, либо имеет бесконечное множество решений.
Метод Лагранжа и Ньютона

Метод Гаусса и Крамера

Для решения системы уравнений с помощью метода Гаусса необходимо привести ее к ступенчатому виду путем элементарных преобразований над уравнениями. Затем, используя обратный ход метода Гаусса, можно найти значения неизвестных.
Метод Крамера основан на вычислении определителей матрицы системы уравнений. Для каждой неизвестной с помощью правила Крамера можно вычислить ее значение как отношение определителя, где вместо столбца коэффициентов данной неизвестной столбец свободных членов, к определителю исходной матрицы.
Вопрос-ответ

Каким образом можно решить систему уравнений 3x + 2y = 4 и x² + 2z³ = 3?
Для решения данной системы уравнений можно использовать различные методы, включая метод подстановки, метод исключения и метод Гаусса. Например, можно сначала выразить x из первого уравнения, подставить это выражение во второе уравнение и затем решить полученное уравнение относительно z. Еще одним вариантом является представление одной переменной через другие две и последующее выражение третьей переменной. Таким образом, решение данной системы требует алгебраических вычислений и умения применять различные методы решения уравнений.
Могут ли возникнуть сложности при решении системы уравнений 3x + 2y = 4 и x² + 2z³ = 3? Как их преодолеть?
В процессе решения данной системы уравнений могут возникнуть сложности, такие как необходимость вычислений с квадратными и кубическими степенями переменных. Для преодоления таких трудностей рекомендуется использовать алгебраические приемы, например, представление одной переменной через другие или применение метода исключения. Также стоит быть внимательным при проведении вычислений, чтобы избежать ошибок. Важно следить за каждым шагом и внимательно анализировать полученные уравнения, чтобы правильно идти к решению.



