Тупоугольный треугольник - один из видов треугольников, где один из углов больше 90 градусов. Высота этого треугольника - линия, проведенная из вершины прямого угла к противоположной стороне. Построение высоты в таком треугольнике может быть выполнено с использованием циркуля и ручки.
Для построения высоты в тупоугольном треугольнике сначала проводится ортоцентр - точка пересечения трех высот треугольника. Затем, используя циркуль, проводится радиус от ортоцентра к вершине тупого угла треугольника. Таким образом, высота строится как перпендикуляр к соответствующей стороне треугольника.
Построение высоты в тупоугольном треугольнике с использованием циркуля позволяет определить точное положение высоты и использовать ее для дальнейших расчетов или построений. Этот метод является точным и эффективным в работе с треугольниками различных форм и размеров.
Как найти высоту в тупоугольном треугольнике
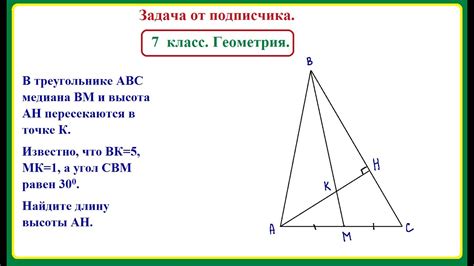
Для нахождения высоты в тупоугольном треугольнике нужно учитывать особенности данного типа треугольников. Высота в таком треугольнике будет вне самого треугольника, перпендикулярно к основанию, проведенному за вершину угла.
Для построения высоты с использованием циркуля выполняется следующий алгоритм:
- Продолжить одну из сторон треугольника за вершину угла, чтобы получился остроугольный треугольник.
- Поставить циркуль в точку продолжения стороны и провести дугу, пересекающую противоположную сторону исходного треугольника.
- Точка пересечения дуги с противоположной стороной будет вершиной построенного перпендикуляра, который и будет высотой тупоугольного треугольника.
Таким образом, высоту тупоугольного треугольника можно построить с использованием циркуля, расширив одну из сторон за вершину и проведя перпендикуляр к основанию треугольника.
Шаг 1: Построение треугольника с помощью циркуля
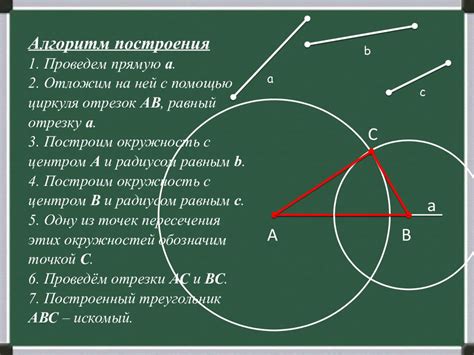
Укажите на бумаге вершину А, Г и В треугольника, используя циркуль для построения окружности каждой вершины.
Соедините вершины прямыми линиями, чтобы получился треугольник. Убедитесь, что треугольник получился тупоугольным, то есть один из углов составляет больше 90 градусов.
Шаг 2: Определение сторон треугольника
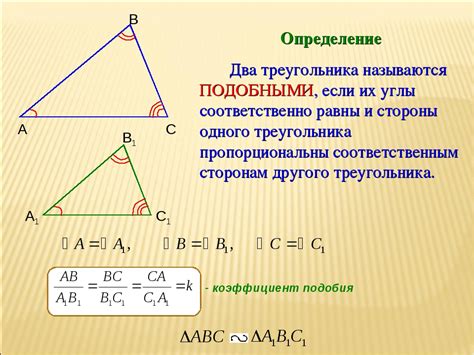
Прежде чем приступить к построению высоты в тупоугольном треугольнике с помощью циркуля, необходимо определить длины его сторон.
Для этого можно воспользоваться формулой Пифагора, если известны две стороны треугольника, или воспользоваться тригонометрическими функциями, если известны углы и одна из сторон.
После определения длин сторон можно продолжать к следующему шагу построения высоты. Важно точно измерить и определить все необходимые параметры для достижения точного результата.
Шаг 3: Нахождение угла треугольника
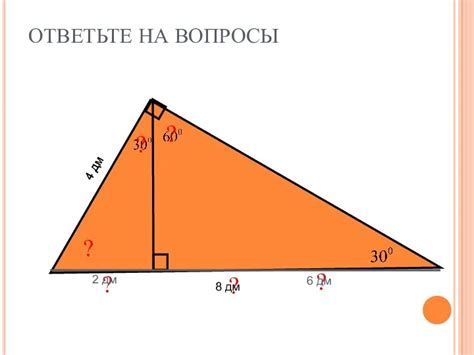
Чтобы найти угол в тупоугольном треугольнике, можно воспользоваться формулой, связывающей длины сторон треугольника с косинусом угла:
cos(∠A) = (b^2 + c^2 - a^2) / (2bc)
Где A - угол, противолежащий стороне a, b и c - длины других двух сторон.
Определив косинус угла A, можно вычислить сам угол, взяв его арккосинус:
∠A = arccos(cos(∠A))
Теперь у вас есть все необходимые данные, чтобы определить угол треугольника. Продолжайте с уверенностью!
Шаг 4: Применение теоремы косинусов для вычисления высоты

Для нахождения высоты тупоугольного треугольника с помощью циркуля необходимо использовать теорему косинусов. Эта теорема позволяет нам выразить высоту через стороны и углы треугольника.
Высота треугольника, проведенная к тупому углу, может быть найдена по формуле:
h = b * sin(A),
где h - высота треугольника, b - сторона, противолежащая тупому углу, A - величина тупого угла.
Используя выражение для синуса тупого угла через косинус острого угла (sin(A) = cos(90°-A)), мы можем выразить высоту через косинус острого угла:
h = b * cos(B),
где h - высота треугольника, b - сторона, противолежащая тупому углу, B - величина острого угла.
Теперь мы можем приступить к расчету высоты тупоугольного треугольника с использованием циркуля, зная стороны и углы треугольника.
Шаг 5: Результат вычисления высоты треугольника
Вопрос-ответ

Как построить высоту тупоугольного треугольника при помощи циркуля?
Для построения высоты тупоугольного треугольника с помощью циркуля проведите дугу с центром в вершине угла, через которую проходит прямая сторона треугольника. Точка пересечения дуги и прямой стороны будет вершиной перпендикуляра от этой вершины к основанию. Соедините вершину треугольника с этой точкой, чтобы получить высоту.
Как построить высоту в треугольнике, если известны только две стороны?
Если известны две стороны треугольника, то высота может быть построена с помощью циркуля, если известен угол при вершине, образованный этими двумя сторонами. Проведите дугу с центром в вершине угла и проходящую через точку пересечения этих двух сторон. Точка пересечения дуги и прямой стороны будет точкой, через которую проходит высота треугольника.
Зачем нужно проводить высоту в тупоугольном треугольнике?
Высота тупоугольного треугольника представляет собой отрезок, проведенный из вершины треугольника к противоположной стороне, перпендикулярно этой стороне. Построение высоты может помочь определить центр окружности, описанной вокруг треугольника и провести дальнейшие геометрические построения и вычисления.



