Определитель матрицы – важное понятие в линейной алгебре, которое позволяет определить её обратимость и вычислить решения систем линейных уравнений. Но что делать, если матрица не является квадратной? Как определить её определитель? В данной статье мы рассмотрим различные методы для нахождения определителя неквадратной матрицы и приведем примеры для наглядного понимания.
Матрица является квадратной, если количество строк равно количеству столбцов. Но что делать, если эти значения не совпадают? В таком случае, матрица считается неквадратной и её определитель не может быть вычислен стандартными методами. Однако существуют специальные подходы, которые позволяют определить определитель для таких матриц.
Продолжение статьи содержит разбор методов вычисления определителя неквадратной матрицы с подробными пошаговыми инструкциями и практическими примерами. Открыть мир линейной алгебры на новом уровне возможно с помощью понимания определения неквадратной матрицы.
Методы поиска определителя
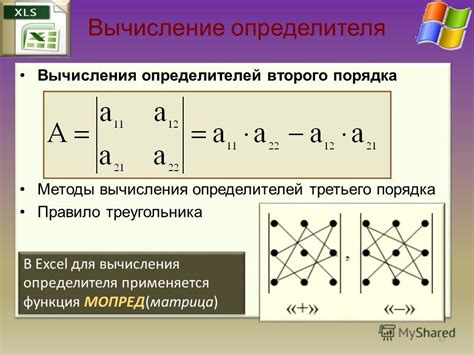
Существуют несколько методов для вычисления определителя матрицы, включая:
| 1. Метод разложения по строке или столбцу. |
| 2. Метод Гаусса. |
| 3. Метод Лапласа (миноров и алгебраических дополнений). |
Каждый из этих методов имеет свои преимущества и недостатки, и выбор конкретного метода зависит от размерности матрицы и доступных вычислительных ресурсов.
Метод Гаусса для неквадратных матриц

Шаги метода Гаусса для неквадратной матрицы аналогичны шагам для квадратной матрицы, с тем отличием, что мы работаем с прямоугольными матрицами. На каждом шаге алгоритма мы выбираем главный элемент и нормируем его строку, затем вычитаем эту строку из оставшихся строк с подходящими коэффициентами.
Пример использования метода Гаусса для неквадратной матрицы:
1 2 3 3 4 5
Применим метод Гаусса для приведения этой матрицы к треугольному виду. Начнем с выбора первого главного элемента (1 в этом случае) и нормализации строки. Затем вычтем первую строку из второй с соответствующими коэффициентами. Процесс продолжаем до получения треугольной матрицы или выявления несовместности системы.
Метод разложения по строке для неквадратных матриц

Для определения определителя неквадратной матрицы можно использовать метод разложения по строке. Этот метод основан на раскрытии определителя по определённой строке или столбцу.
Предположим, что у нас есть матрица размером m x n, где m ≠ n. Для нахождения определителя данной матрицы необходимо выбрать строку (или столбец), разложить определитель по этой строке (или столбцу) и вычислить определитель матрицы меньшего порядка.
Пример: рассмотрим матрицу 3 x 2:
A =
| 1 | 2 |
| 3 | 4 |
| 5 | 6 |
Для вычисления определителя данной матрицы по определённой строке (например, первой) необходимо:
- Выбрать строку по которой будем раскрывать определитель, например, первую строку (1, 2).
- Дальше, раскрываем определитель по первой строке: det(A) = 1 * det(B) - 2 * det(C), где B и C - матрицы меньшего порядка, полученные при удалении первой строки и соответствующих столбцов.
- Вычисляем определители матриц меньшего порядка и подставляем в формулу. Например, определитель матрицы B 2 x 2 будет равен: det(B) = 4 - 3 = 1.
- Заменяем значения в формуле и находим окончательное значение определителя для данной строки.
Таким образом, метод разложения по строке для неквадратных матриц позволяет вычислить определитель матрицы, не являющейся квадратной, путем разложения по определенной строке или столбцу.
Примеры нахождения определителя

Рассмотрим матрицу 2x2:
\[ A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \]
Определитель данной матрицы вычисляется по формуле:
\[ \text{det}(A) = 1 \cdot 4 - 2 \cdot 3 = 4 - 6 = -2 \]
Таким образом, определитель матрицы \( A \) равен -2.
Рассмотрим матрицу 3x3:
\[ B = \begin{bmatrix} 2 & 1 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix} \]
Определитель матрицы \( B \) можно найти с помощью разложения по любой строке или столбцу. Например, разложим по первой строке:
\[ \text{det}(B) = 2 \cdot \text{det}\begin{pmatrix} 5 & 6 \\ 8 & 9 \end{pmatrix} - 1 \cdot \text{det}\begin{pmatrix} 4 & 6 \\ 7 & 9 \end{pmatrix} + 3 \cdot \text{det}\begin{pmatrix} 4 & 5 \\ 7 & 8 \end{pmatrix} \]
Вычисляя определители миноров, получим:
\[ \text{det}(B) = 2 \cdot (5 \cdot 9 - 6 \cdot 8) - 1 \cdot (4 \cdot 9 - 6 \cdot 7) + 3 \cdot (4 \cdot 8 - 5 \cdot 7) = 2 \cdot 9 - 1 \cdot 3 + 3 \cdot 1 = 18 - 3 + 3 = 18 \]
Таким образом, определитель матрицы \( B \) равен 18.
Вопрос-ответ

Что такое определитель матрицы?
Определитель матицы - это численная характеристика, которая вычисляется для квадратной матрицы. Он помогает определить, обратима ли матрица, и решить систему линейных уравнений. Определитель обозначается символом det(A) или |A|.
Как найти определитель матрицы методом Гаусса?
Для нахождения определителя матрицы методом Гаусса нужно привести матрицу к треугольному виду с помощью элементарных преобразований строк. Затем определитель вычисляется как произведение элементов на главной диагонали умноженное на коэффициент перестановки строк.
Как найти определитель матрицы по определению?
Определитель матицы можно найти по определению через миноры и алгебраические дополнения. Для этого необходимо выбрать любую строку или столбец матрицы, выделить минор, определить его определитель, а затем вычислить определитель исходной матрицы через сумму произведений элементов на соответствующие алгебраические дополнения.
Приведите пример вычисления определителя неквадратной матрицы.
Для примера возьмем матрицу размером 3x2: {{1, 2}, {3, 4}, {5, 6}}. Для нахождения определителя данной матрицы можно использовать формулу det(A) = a11*a22 - a12*a21, где aij - элемент матрицы на пересечении i-й строки и j-го столбца. Таким образом, определитель матрицы будет равен (1*4 - 2*3) = -2.



