Равнобедренный треугольник - это такой треугольник, у которого две стороны равны между собой. Это означает, что у треугольника две равные угловые стороны и одна неравная основа.
Для того чтобы определить сторону равнобедренного треугольника, можно воспользоваться различными методами. Один из них - использование теоремы Пифагора. Если известна длина основы и высоты треугольника, можно вычислить длину боковой стороны, которая будет равна корню квадратному из разницы квадрата гипотенузы и квадрата половины основы.
Также можно воспользоваться свойством равнобедренного треугольника, что смежные углы при основании равны. Зная длину основы и высоту, можно разделить основу пополам и применить тригонометрические функции для вычисления длины боковой стороны.
Способы определения сторон равнобедренного треугольника

Существует несколько способов определения сторон равнобедренного треугольника:
1. По величине углов: В равнобедренном треугольнике два угла при основании равны, а третий угол – вершина – меньше.
2. По длине сторон: В равнобедренном треугольнике две стороны, выходящие из вершины равны, а третья – основание – меньше.
3. По симметрии: Равнобедренный треугольник симметричен относительно своей высоты, которая является медианой и биссектрисой одновременно.
Взаимное равенство сторон и углов
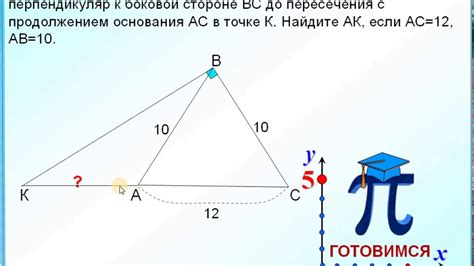
Формула для вычисления стороны
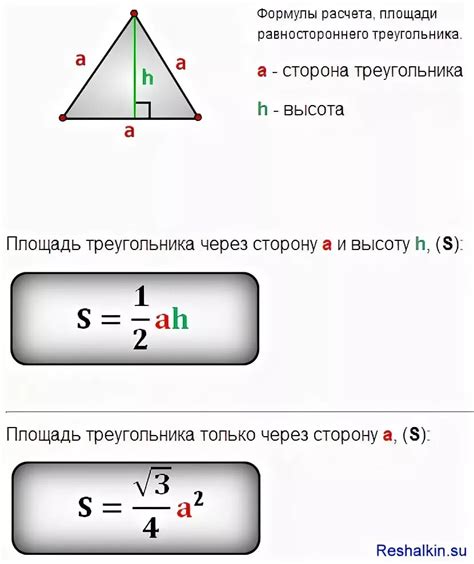
Если известна длина оснований равнобедренного треугольника и его высота, то можно вычислить длину стороны треугольника по формуле:
Сторона равнобедренного треугольника = √(б^2 - (основание/2)^2), где б - длина основания.
Использование высоты и медианы
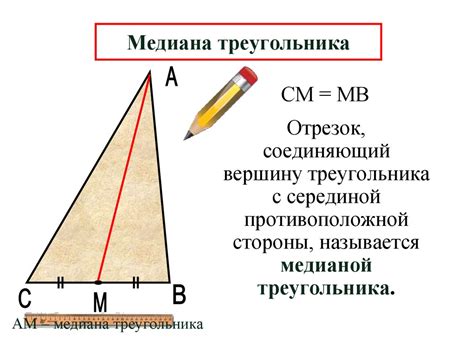
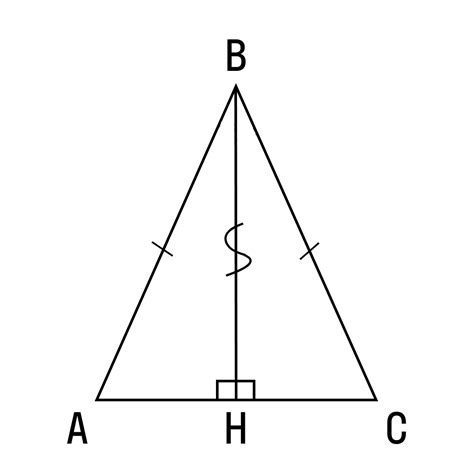
Высота и медиана равнобедренного треугольника могут использоваться для определения его сторон. Рассмотрим равнобедренный треугольник ABC, где AB = AC.
| Элемент | Определение |
| Высота | Высота треугольника соединяет вершину угла, противолежащего большей стороне (BC), с серединой этой стороны. Высота перпендикулярна стороне BC и делит треугольник на два равных прямоугольных треугольника. |
| Медиана | Медиана треугольника соединяет вершину угла с серединой противоположной стороны. В равнобедренном треугольнике медиана также является высотой и делит треугольник на два равных треугольника. |
Таким образом, по длине высоты (медианы) и базы равнобедренного треугольника можно определить его стороны, используя свойства треугольников и теорему Пифагора.
Сочетание свойств равнобедренного треугольника
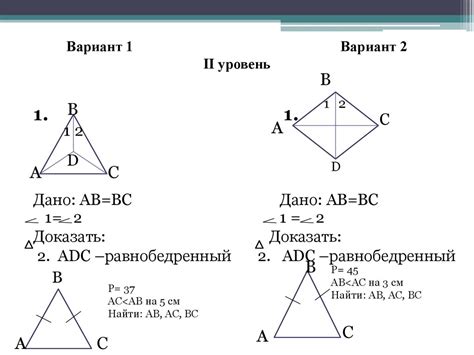
Равнобедренный треугольник обладает несколькими характерными свойствами, которые позволяют быстро и легко определить его стороны и углы:
- В равнобедренном треугольнике две стороны равны между собой, т.е. AB = AC, где AB и AC - боковые стороны треугольника, а BC - основание.
- Углы, противолежащие равным сторонам, также равны. В данном случае угол B = углу C.
- Медианы, проведенные к основанию треугольника из вершин, совпадают и делят основание пополам.
- Основаниями равнобедренного треугольника являются равные стороны. Таким образом, длина основания равна половине периметра треугольника.
Измерение диагоналей и углов
Для определения стороны равнобедренного треугольника важно измерить две диагонали. Проведите линию от вершины, где сходятся стороны равнобедренного треугольника, до противоположного основания. Эта линия пройдет через центр и будет являться диагональю. Измерьте длину этой диагонали с помощью линейки или шнура.
После этого измерьте углы при основании равнобедренного треугольника. Они должны быть равными. Это можно сделать с помощью транспортира или другого измерительного инструмента. Если углы при основании равны, то треугольник равнобедренный. Если же они отличаются, то треугольник неравнобедренный.
| Измерение диагонали | Измерение углов |
|---|---|
| Измерить длину диагонали с помощью линейки или шнура | Измерить углы при основании с помощью транспортира |
Применение теоремы Пифагора

Применение теоремы Пифагора позволяет определить стороны равнобедренного треугольника, если нам известна длина его основания. Например, если известна длина основания треугольника и его высота, то можно рассчитать длину боковой стороны, применяя теорему Пифагора.
Использование тригонометрических функций

Для определения сторон равнобедренного треугольника можно использовать тригонометрические функции. Например, если известен угол при основании равнобедренного треугольника, то для определения сторон можно использовать функции синуса, косинуса или тангенса.
Пусть угол при основании равен α. Тогда сторона треугольника, противолежащая этому углу, равна a, а катеты, прилегающие к углу α, равны b. Тогда можно записать:
- sin(α) = b / a
- cos(α) = a / 2
- tan(α) = b / (a / 2)
С помощью этих формул можно определить стороны равнобедренного треугольника, зная угол при основании и одну из сторон или катетов.
Особенности равнобедренного треугольника
| Признак равнобедренного треугольника | Свойства |
|---|---|
| Основание и стороны | Две стороны равны между собой, третья сторона – основание |
| Углы при основании | Два угла при основании равны |
Вопрос-ответ

Как определить сторону равнобедренного треугольника?
В равнобедренном треугольнике две стороны равны, а третья сторона, противолежащая основанию, может быть различной. Для определения стороны равнобедренного треугольника нужно знать значения двух равных сторон и угла между ними. С помощью закона косинусов можно найти длину любой стороны треугольника.
Каким образом можно найти высоту равнобедренного треугольника?
Чтобы найти высоту равнобедренного треугольника, можно воспользоваться тем фактом, что она будет перпендикулярна к основанию треугольника. Также можно воспользоваться теоремой Пифагора или теоремой косинусов в общем случае равнобедренного треугольника.
Что нужно знать о равнобедренном треугольнике для решения задачи?
Для решения задачи, связанной с равнобедренным треугольником, необходимо знать значения сторон и углов данного треугольника, а также быть в состоянии применить теоремы о равнобедренном треугольнике, например, теорему о средней линии, теорему косинусов или теорему Пифагора.



