Ромб – это геометрическая фигура с четырьмя равными сторонами. Высота ромба – это перпендикуляр, проведенный от одной из вершин ромба к противоположной стороне. Нахождение высоты ромба по периметру и площади требует применения определенных математических формул и методов расчета.
Для того чтобы найти высоту ромба, зная его периметр и площадь, можно воспользоваться следующими формулами:
1. Формула для высоты ромба по его площади: H = S / d, где H – высота ромба, S – площадь ромба, d – диагональ ромба.
2. Формула для высоты ромба по его периметру и длинам диагоналей: H = 2 * S / (d1 + d2), где d1 и d2 – длины двух диагоналей ромба.
Математические формулы и методы расчета высоты ромба
Высота ромба может быть найдена с использованием следующей формулы:
h = 2 * S / d
Где:
h - высота ромба
S - площадь ромба
d - длина диагонали ромба
Также, используя формулу для расчета периметра ромба, можно найти высоту, зная площадь:
h = 4 * S / P
Где:
P - периметр ромба
Эти математические формулы и методы помогут быстро и точно найти высоту ромба, при известных параметрах площади, длины диагонали и периметра.
Определение высоты ромба через периметр
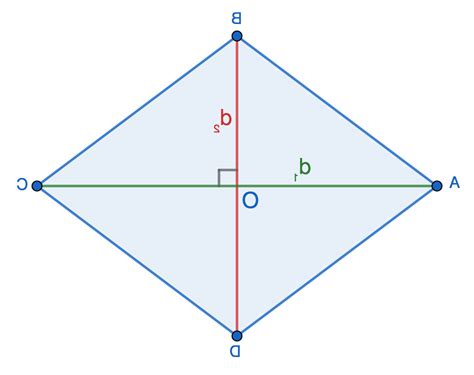
Для определения высоты ромба через его периметр можно воспользоваться следующей формулой:
| Высота ромба | h = \dfrac{2 \cdot S}{a} |
Где h - высота ромба, S - площадь ромба, a - длина одной из сторон ромба.
Формула расчета высоты ромба через периметр
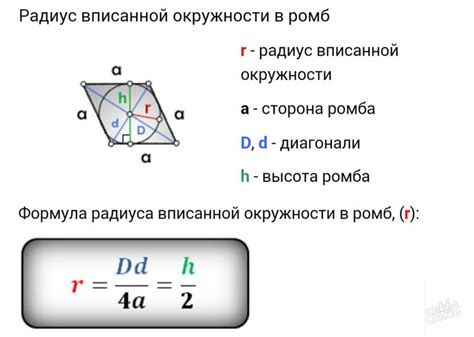
Для вычисления высоты ромба через его периметр применяется следующая формула:
Высота ромба = Периметр ромба / (2 * √3)
Где Периметр ромба - сумма длин всех его сторон.
Примеры вычисления высоты ромба по периметру
Для нахождения высоты ромба по периметру можно воспользоваться следующим примером:
Пусть периметр ромба равен 24 см. Для начала найдем длину одной его стороны, поделив периметр на 4: 24 / 4 = 6 см.
Зная длину стороны ромба, с помощью формулы для высоты ромба, где h = S / a (h - высота, S - площадь, a - длина стороны), найдем высоту ромба.
Например, если площадь ромба равна 36 кв. см, то высота будет h = 36 / 6 = 6 см.
Определение высоты ромба через площадь
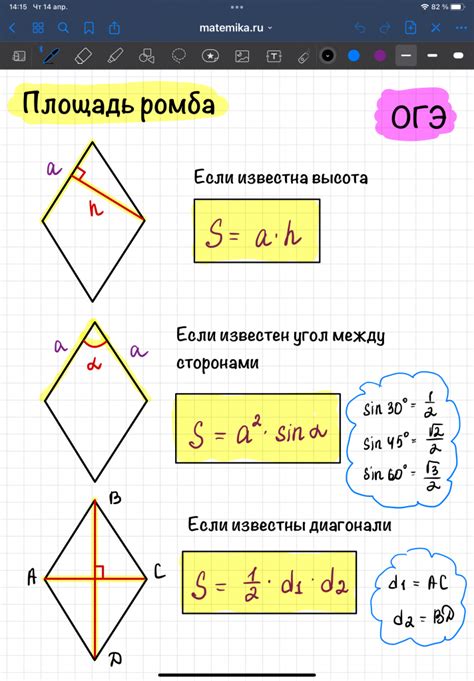
h = 2S / d
где:
h - высота ромба;
S - площадь ромба;
d - длина диагонали ромба.
Для решения данной задачи необходимо знать площадь ромба и длину одной из его диагоналей. Подставив известные значения в формулу, можно легко определить высоту ромба.
Методы расчета высоты ромба по площади
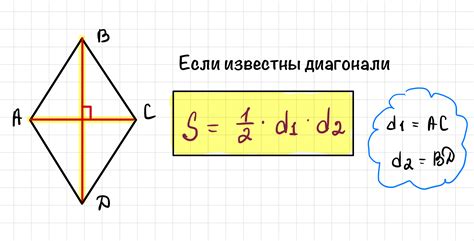
Для нахождения высоты ромба по площади можно воспользоваться следующей формулой:
h = | 2 * S / d |
где:
h - высота ромба;
S - площадь ромба;
d - диагональ ромба.
Сначала найдем диагональ ромба, а затем, используя данную формулу, рассчитаем высоту ромба.
Формула расчета высоты ромба через площадь
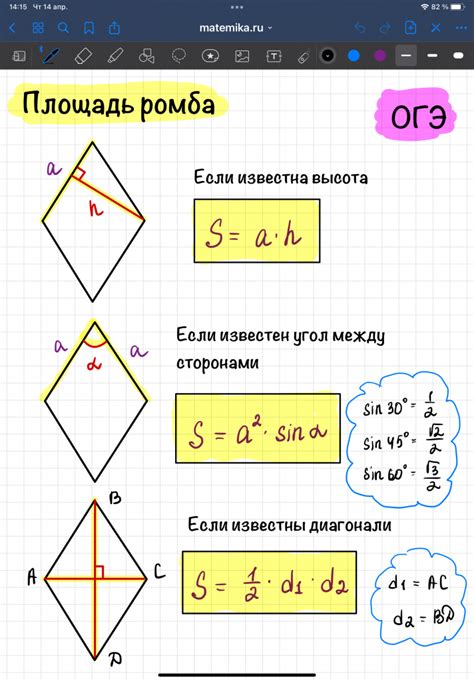
Для нахождения высоты ромба, зная его площадь, можно воспользоваться следующей формулой:
| h = | 2 * S | , где | S - площадь ромба. |
Вопрос-ответ

Какой метод можно использовать для расчета высоты ромба по известной площади?
Для расчета высоты ромба по известной площади можно воспользоваться формулой: h = 2*Площадь/Диагональ. При этом необходимо знать площадь ромба и длину одной из его диагоналей. Подставив известные значения в формулу, можно определить высоту ромба.
Если известен периметр ромба, как можно найти его высоту?
Для определения высоты ромба по известному периметру можно воспользоваться формулой: h = Площадь/Полупериметр. Необходимо знать площадь ромба и его периметр. Подставив значения в формулу, можно найти высоту ромба.
Какие математические методы можно применить для нахождения высоты ромба?
Для расчета высоты ромба можно использовать различные математические методы, включая формулы, основанные на площади и периметре ромба. Также можно воспользоваться теоремами о ромбе, связанными с его диагоналями. Например, высота ромба можно найти, зная одну из его диагоналей. Методы расчета выбираются в зависимости от известных данных и задачи, которую необходимо решить.



