Перпендикуляр - это прямая или отрезок, который образует прямой угол с другой прямой или плоскостью. Перпендикуляр к плоскости можно построить из точки, находящейся за пределами этой плоскости. Этот метод находит применение в различных областях, таких как геометрия, инженерия и архитектура.
Существует несколько способов построения перпендикуляра к плоскости из точки: используя угол между перпендикуляром и плоскостью, проводя перпендикулярный отрезок из точки к плоскости или пользуясь уравнениями плоскости и прямой.
В данной статье мы рассмотрим каждый из этих методов детально, проиллюстрируем их на примерах и объясним основные принципы построения перпендикуляра к плоскости из точки.
Постройка перпендикуляра
Для построения перпендикуляра к плоскости из точки необходимо выполнить следующие шаги:
- Выберите точку, из которой нужно построить перпендикуляр.
- Найдите проекцию выбранной точки на плоскость, к которой будет строиться перпендикуляр.
- Проведите линию из найденной проекции точки, перпендикулярную плоскости.
- Точка пересечения этой линии с плоскостью будет являться конечной точкой перпендикуляра.
Таким образом можно построить перпендикуляр к произвольной плоскости из заданной точки. Этот метод широко применяется в геометрии и инженерии для решения различных задач.
Перпендикулярная плоскость: методика
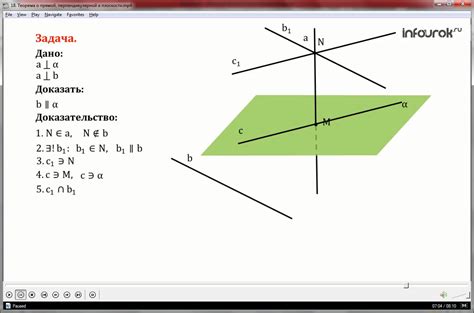
Для построения перпендикулярной плоскости из точки необходимо выполнить следующие шаги:
- Выберите точку и указанную плоскость.
- Из точки проведите прямую, перпендикулярную плоскости.
- Выберите вторую точку на этой перпендикулярной линии.
- Проведите плоскость, проходящую через обе точки и точку начальной плоскости.
Таким образом, вы построите перпендикулярную плоскость к указанной из точки.
Как найти точку пересечения?

Для того чтобы найти точку пересечения прямой с плоскостью, необходимо решить систему уравнений, состоящую из уравнения плоскости и уравнения прямой. Первым шагом найдем уравнение прямой, проходящей через заданную точку перпендикулярно плоскости. Затем подставим это уравнение в уравнение плоскости и найдем координаты точки пересечения. В результате получим точку пересечения прямой с плоскостью.
Алгоритм с применением угла
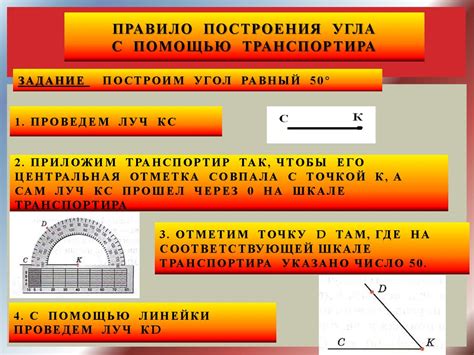
- Проведите линию через заданную точку и точку на плоскости, к которой нужно построить перпендикуляр.
- Поставьте циркуль в заданной точке и отметьте на проведенной линии точку, находящуюся на расстоянии, равном заданному отрезку, от начальной точки.
- Создайте угол в этой точке так, чтобы он был равным 90 градусам.
- Проведите линию, проходящую через начальную точку и точку, а также через точку под углом.
Таким образом будет построен перпендикуляр к плоскости из заданной точки с использованием угла.
Точка пересечения: геометрическая точка зрения
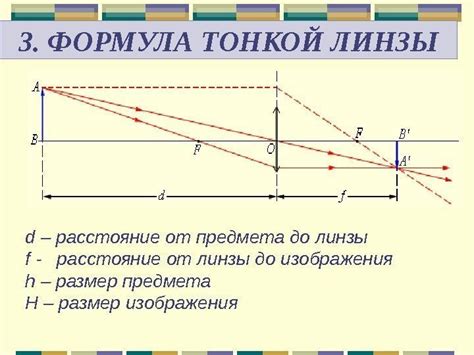
Для определения точки пересечения в геометрии можно использовать различные методы, например, метод графического построения, метод решения систем уравнений и т. д. Важно учитывать особенности задачи и выбирать наиболее подходящий метод для определения точки пересечения.
Точка пересечения может быть определена как точка, в которой сообщаются необходимые условия для построения перпендикуляра к плоскости из данной точки. Эта точка может играть ключевую роль в решении геометрических задач и помочь получить точный результат.
| Примеры использования | Применение в практике |
|---|---|
| Построение перпендикуляра к плоскости из точки | Определение расстояния от точки до плоскости |
| Построение прямой, проходящей через точку и перпендикулярной данной плоскости | Построение пересекающихся прямых и углов |
Проекция перпендикуляра на плоскость
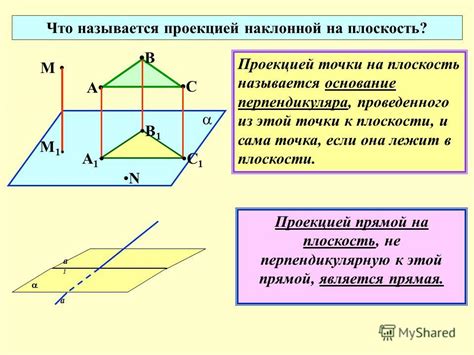
Для построения проекции перпендикуляра из точки на плоскость необходимо следовать определенным шагам. Сначала проведите линию из точки, проходящую через плоскость под углом 90 градусов. Пересечение этой линии с плоскостью даст точку проекции перпендикуляра.
При этом важно учитывать, что проекция перпендикуляра является кратчайшим расстоянием от точки до плоскости. Этот метод позволяет определить точку на плоскости, в которой перпендикуляр к плоскости, исходящий из точки, встречает ее.
Таким образом, построение проекции перпендикуляра на плоскость из точки позволяет определить точку на плоскости, через которую проходит перпендикуляр из данной точки к плоскости.
Решение задач с построением перпендикуляра
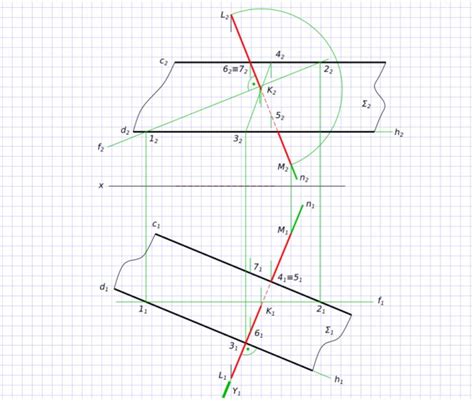
При решении задач по построению перпендикуляра к плоскости из точки необходимо учитывать следующие шаги:
| 1. | Определить координаты точки, из которой требуется построить перпендикуляр. |
| 2. | Найти уравнение плоскости, к которой нужно построить перпендикуляр. |
| 3. | Найти вектор нормали к плоскости, который будет перпендикулярен этой плоскости. |
| 4. | Построить отрезок, начинающийся в заданной точке и направленный вдоль вектора нормали. |
| 5. | Этот отрезок будет являться перпендикуляром к заданной плоскости из заданной точки. |
Практическое применение алгоритма
Алгоритм построения перпендикуляра к плоскости из точки найдет свое практическое применение в различных областях, таких как геометрия, инженерное дело, архитектура и дизайн. Например, в архитектуре часто требуется построить перпендикулярный элемент от определенной точки для выравнивания структуры здания или улучшения эстетики. Точное вычисление перпендикуляра поможет добиться точности и качества в проекте.
| Пример | Описание |
|---|---|
| Геодезия | В геодезии перпендикуляр к плоскости из точки используется для определения точного положения объектов на местности, земледелия и строительства. |
| Инженерное дело | В инженерном деле алгоритм строит перпендикуляр для расчета расстояний, проектирования дорог и инфраструктуры. |
Методы обобщенной задачи

Шаг 1: Найти нормаль к плоскости. Для этого можно воспользоваться уравнением плоскости и определить коэффициенты A, B, C (если плоскость задана уравнением Ax + By + Cz + D = 0, то нормаль к плоскости будет вектор [A, B, C]).
Шаг 2: Построить вектор от точки до произвольной точки на плоскости. Этот вектор может быть любым направляющим вектором плоскости, например, [A, B, -C].
Шаг 3: Найти проекцию этого вектора на нормаль к плоскости. Для этого используется формула проекции вектора b на вектор a: proj_a(b) = (b*a)/|a| * a.
Полученная проекция будет направлена в сторону нормали к плоскости. Она и будет задавать искомый перпендикуляр к плоскости из данной точки.
Трюки и особенности при построении

При построении перпендикуляра к плоскости из точки стоит обратить внимание на несколько трюков и особенностей.
1. Определение плоскости: Важно точно определить плоскость, к которой нужно построить перпендикуляр. Известные точки или прямые на плоскости могут помочь в этом.
2. Выбор метода: Существуют различные методы построения перпендикуляра, например, с использованием транспортира или чертежного инструмента. Выберите подходящий метод с учетом сложности задачи.
3. Точность и аккуратность: Построение перпендикуляра требует точности и внимания к деталям. Не торопитесь и проверяйте каждый шаг.
4. Проверка результатов: После завершения построения перпендикуляра важно проверить его правильность. Используйте известные геометрические свойства, чтобы убедиться в корректности выполненной работы.
Следуя этим трюкам и особенностям, вы сможете успешно построить перпендикуляр к плоскости из заданной точки.
Вопрос-ответ

Как построить перпендикуляр к плоскости из точки?
Для построения перпендикуляра к плоскости из точки необходимо провести прямую, которая будет перпендикулярна плоскости и проходить через эту точку. Это можно сделать различными способами, например, с использованием углов или векторов.
Какие методы можно использовать для построения перпендикуляра к плоскости из точки?
Для построения перпендикуляра к плоскости из точки можно использовать метод проекций, метод векторного произведения, метод углового поворота и другие геометрические подходы.
Для чего нужно строить перпендикуляр к плоскости из точки?
Перпендикуляр к плоскости из точки строят, когда необходимо определить направление перпендикулярной прямой или плоскости, проходящей через точку. Это часто используется в геометрии, строительстве, архитектуре и других областях.
Можно ли построить перпендикуляр к плоскости из точки без использования геометрических инструментов?
Да, можно построить перпендикуляр к плоскости из точки без использования геометрических инструментов, но для этого потребуется знание соответствующих математических методов и алгоритмов. Например, можно воспользоваться вычислениями на бумаге или компьютере.
Каким образом определяется расстояние от точки до плоскости, к которой проведен перпендикуляр?
Расстояние от точки до плоскости, к которой проведен перпендикуляр, определяется как длина перпендикуляра, проведенного из точки на плоскости. Это расстояние вычисляется по формуле, которая зависит от координат точки и уравнения плоскости.



