Обратная матрица – это такая матрица, которая при умножении на исходную матрицу дает единичную матрицу. Нахождение обратной матрицы является важной задачей в линейной алгебре и математике в целом. В данной статье мы рассмотрим методы и алгоритмы для нахождения обратной матрицы размером 3x3.
Для того чтобы найти обратную матрицу 3x3, необходимо следовать определенному алгоритму, использующему определители, алгебраические дополнения и матрицу союзных элементов. В данном руководстве мы разберем все шаги этого процесса и предоставим примеры вычислений для более понятного представления.
Поиск обратной матрицы 3x3

Для поиска обратной матрицы размером 3x3 необходимо выполнить определенные шаги:
- 1. Вычислить определитель исходной матрицы.
- 2. Найти алгебраические дополнения для каждого элемента матрицы.
- 3. Транспонировать матрицу алгебраических дополнений.
- 4. Полученную матрицу разделить на определитель исходной матрицы.
После выполнения этих шагов вы получите обратную матрицу 3x3, которая будет являться обратной к исходной.
Шаг 1: Определение детерминанта матрицы
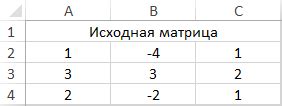
Определитель матрицы A обозначается как det(A) или |A|, и для матрицы 3x3 вычисляется как сумма произведений элементов первой строки на их миноры (определители 2x2, полученные после вычеркивания соответствующей строки и столбца).
Определитель матрицы A размерности 3x3 можно выразить формулой:
|A| = a(ei − fh) − b(di − fg) + c(dh − eg)
Где a, b, c, d, e, f, g, h, i - элементы матрицы A.
Шаг 2: Вычисление алгебраических дополнений

Шаг 3: Формирование обратной матрицы

Для того чтобы найти обратную матрицу, следует выполнить следующие действия:
- Вычислить определитель исходной матрицы согласно формуле.
- Найти алгебраические дополнения для каждого элемента матрицы.
- Транспонировать матрицу из алгебраических дополнений.
- Разделить каждый элемент полученной матрицы на значение определителя исходной матрицы.
Полученная матрица будет являться обратной к исходной.
Вопрос-ответ

Как можно найти обратную матрицу 3x3?
Для того чтобы найти обратную матрицу 3x3, необходимо вычислить определитель исходной матрицы. Далее следует найти алгебраические дополнения к элементам матрицы, транспонировать матрицу из алгебраических дополнений и поделить на определитель исходной матрицы. Таким образом, обратная матрица 3x3 вычисляется с помощью математических операций, которые позволяют найти обратную матрицу для исходной.
Можете привести пример вычисления обратной матрицы 3x3?
Конечно, давайте рассмотрим матрицу A размером 3x3: A = {{1, 2, 3}, {0, 1, 4}, {5, 6, 0}}. Сначала найдем определитель матрицы det(A) = 1*(1*0 - 4*6) - 2*(0*0 - 4*5) + 3*(0*6 - 1*5) = 1*(-24) - 2*(-20) + 3*(-5) = -24 + 40 - 15 = 1. Далее, найдем алгебраические дополнения для каждого элемента матрицы, транспонируем их, а затем делим на определитель. Полученная обратная матрица будет обозначена как A^(-1).
Зачем нужно находить обратную матрицу 3x3?
Обратная матрица является важным понятием в линейной алгебре, так как она позволяет решать системы линейных уравнений, вычислять решения линейных дифференциальных уравнений, находить обратные преобразования и многое другое. Наличие обратной матрицы также позволяет решать задачи нахождения обратного масштабирования, поворота и смещения объектов на плоскости и в пространстве.



