Сканф (сокращение от сократимой дисъюнктивной нормальной формы) и сднф (сокращение от сократимой конъюнктивной нормальной формы) являются важными понятиями в логике и теории вычислений. Часто они используются для упрощения булевых функций и улучшения их читаемости.
Чтобы создать сканф, необходимо преобразовать булеву функцию в дизъюнктивную нормальную форму, а затем выполнить определенные операции сокращения. А для сднф - булева функция должна быть преобразована в конъюнктивную нормальную форму, после чего применяются операции сокращения.
В данной статье мы подробно рассмотрим, как создать сканф и сднф, шаг за шагом. Мы покажем основные правила и методы преобразования булевых функций в нормальные формы, а также подробные примеры и иллюстрации для лучшего понимания процесса.
Подготовка к созданию СКАНФ и СДНФ
Прежде чем приступить к созданию СКАНФ (сокращенной конъюнктивной нормальной формы) и СДНФ (сокращенной дизъюнктивной нормальной формы), необходимо подготовить набор исходных данных.
Для этого следует выполнить следующие шаги:
- Определить булевы переменные, которые будут участвовать в логическом выражении.
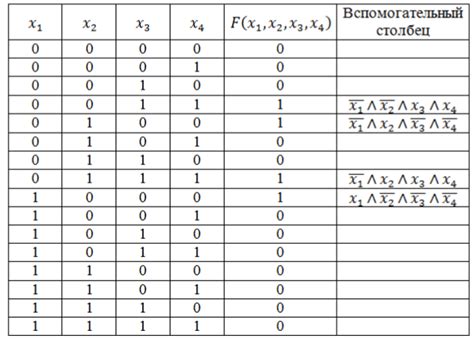
- Составить истинную таблицу истинности для всех возможных комбинаций значений булевых переменных.
- Изучить логическое выражение или условие, по которому производится переход к созданию СКАНФ и СДНФ.
После выполнения этих шагов можно переходить к созданию самой СКАНФ и СДНФ на основе исходных данных.
Выбор логической функции
Перед тем как создать СКАНФ и СДНФ, необходимо определиться с логической функцией, которую мы будем преобразовывать. Логическая функция может быть задана в виде таблицы истинности или логического выражения.
Если логическая функция задана в виде таблицы истинности, то необходимо проанализировать данные и выделить минтермы или макстермы.
Если функция дана в виде логического выражения, то необходимо ее упростить до дизъюнктивной или конъюнктивной нормальной формы. Затем можно построить таблицу истинности и выделить минтермы или макстермы.
Определение набора переменных

Переменные представляют собой набор символов, цифр и специальных знаков, которые могут принимать различные значения. Для определения набора переменных в сканф и сднф необходимо учитывать алфавит, который состоит из различных букв и цифр.
Каждая переменная может принимать одно из двух значений: 0 или 1. Набор всех возможных комбинаций значений переменных называется множество истинности. Для определения этого набора необходимо перечислить все возможные комбинации значений переменных.
Например, если у нас есть две переменные A и B, то множество истинности будет содержать 4 комбинации: (0, 0), (0, 1), (1, 0), (1, 1). Таким образом, определение набора переменных позволяет задать все возможные варианты значений переменных для дальнейшего построения сканф и сднф.
Создание СКАНФ

СКАНФ (сокращение от совершенной конъюнктивной нормальной формы) представляет собой конъюнкцию элементарных дизъюнкций, в которых присутствует каждая переменная или ее отрицание ровно один раз. Для создания СКАНФ необходимо выполнить следующие шаги:
1. Представить логическую функцию в виде таблицы истинности.
2. Определить все нулевые строки таблицы.
3. Преобразовать нулевые строки в элементарные дизъюнкции.
4. Объединить элементарные дизъюнкции в конъюнкцию.
5. Полученная конъюнкция будет являться СКАНФ для данной логической функции.
Таблица истинности
Определение минтермов

Вопрос-ответ




