Медиана правильного треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Она является одной из важных характеристик треугольника и имеет свою формулу для вычисления.
Формула для вычисления медианы правильного треугольника: медиана равна половине длины соседней стороны треугольника.
Например, если мы имеем правильный треугольник со стороной длиной 6 сантиметров, то его медиана равна 3 сантиметрам.
Формула медианы треугольника
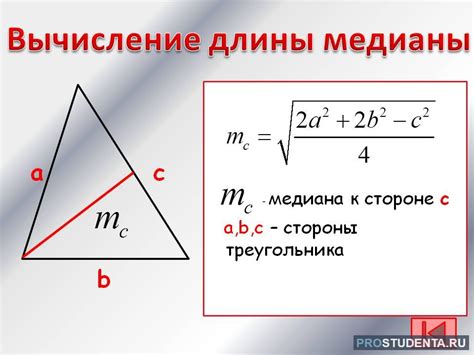
Формула для вычисления медианы в прямоугольном треугольнике, где a и b - катеты, c - гипотенуза:
| Медиана медиана | Формула |
|---|---|
| Из вершины к катету | amc/2 |
| Из середины катета | bmc/2 |
| Из вершины гипотенузы | sqrt(2)/2*c |
Как вычислить медиану треугольника
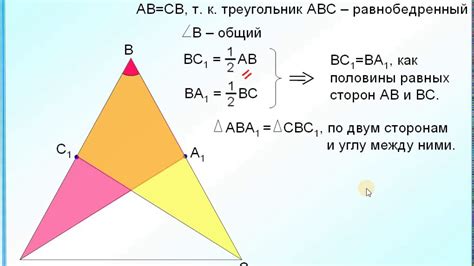
Для вычисления медианы правильного треугольника можно воспользоваться формулой:
- Найдите длину стороны треугольника.
- Рассчитайте высоту как половину произведения стороны на √3 (в случае правильного треугольника).
- Медиана равна половине длины стороны треугольника.
Например, если сторона треугольника равна 6, то высота будет равна 6*√3/2=3√3, а медиана равна 6/2=3.
Примеры расчета медианы треугольника

Для правильного треугольника со стороной a = 5 единиц, медиана, проведенная к стороне a, равна половине длины этой стороны, то есть 2.5 единиц.
Для треугольника со сторонами b = 6 единиц и c = 8 единиц, медиана, проведенная к стороне b, равна корню квадратному из суммы квадратов оставшихся сторон (c^2 + a^2), что равно корню квадратному из 164 и примерно равно 12.81 единиц.
Формула медианы правильного треугольника
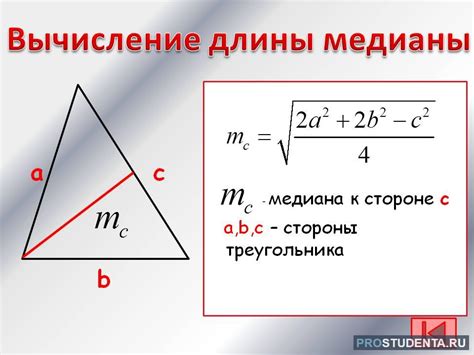
Медиана = 0.5 * √(2 * (a^2 + b^2) - c^2), где a, b, c - стороны треугольника.
Особенности вычисления медианы правильного треугольника
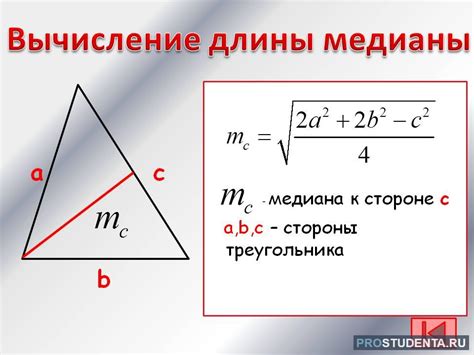
Медиана правильного треугольника, проведенная из вершины прямого угла к гипотенузе, делит ее на две равные части.
Пример: Пусть длина гипотенузы прямоугольного треугольника равна 10 см. Медиана, проведенная из вершины прямого угла к гипотенузе, будет равна 5 см.
Для вычисления длины медианы правильного треугольника можно использовать отношение Пифагора: медиана равна половине гипотенузы.
Подсчет медианы правильного треугольника по формуле
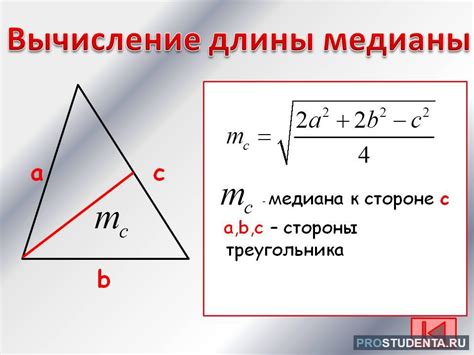
Для вычисления медианы правильного треугольника используется формула:
м = √(a^2 + b^2)/2,
где a и b - длины катетов (сторон) правильного треугольника.
Например, если в правильном треугольнике катеты равны 3 и 4, то медиана будет:
м = √(3^2 + 4^2)/2 = √(9 + 16)/2 = √25/2 = 5/2 = 2,5.
Примеры вычисления медианы правильного треугольника
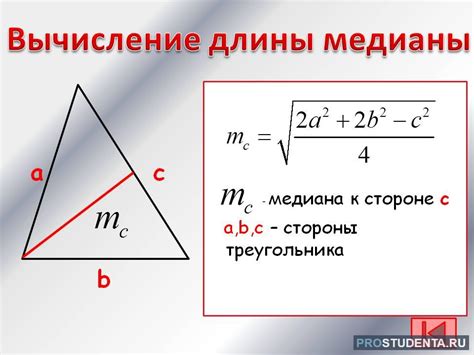
Рассмотрим примеры вычисления медианы правильного треугольника:
- Пример 1: Пусть сторона правильного треугольника равна 6 см. Найдем длину медианы, проведенной к основанию треугольника. Для этого воспользуемся формулой: медиана = √(2a² - b²)/2, где a - сторона треугольника, b - основание. В нашем случае, a=6 см. Подставляя значения, получаем: медиана = √(2*6² - 6²)/2 = √(2*36 - 36)/2 = √(72 - 36)/2 = √36/2 = 6/2 = 3 см.
- Пример 2: Допустим, сторона правильного треугольника равна 10 см. Найдем длину медианы, проведенной к стороне треугольника. Используем формулу: медиана = √(3a²)/2, где a - сторона треугольника. Подставляя значения, получаем: медиана = √(3*10²)/2 = √(3*100)/2 = √300/2 ≈ √150 ≈ 12,25 см.
Вопрос-ответ

Какая формула для вычисления медианы правильного треугольника?
Медиана правильного треугольника с вершиной у основания равна половине длины основания. То есть формула для вычисления медианы равна m = a/2, где a - длина основания.
Как найти медиану правильного треугольника, если известна длина основания?
Для этого просто нужно взять длину основания и разделить её на 2. Например, если основание треугольника равно 10 см, то медиана будет равна 5 см.
Какие примеры вычисления медианы правильного треугольника можно привести?
Пример вычисления медианы правильного треугольника: если сторона треугольника равна 12 см, то медиана, проведенная к этой стороне, будет равна 6 см.



