Среди множества математических формул, одна из особенно интересных и полезных является формула для вычисления разности квадрата синуса и квадрата косинуса. Эта формула позволяет легко и эффективно находить разность данных тригонометрических функций и часто применяется в различных математических задачах.
Формула для вычисления разности квадрата синуса и квадрата косинуса имеет следующий вид: sin^2(x) - cos^2(x) = -cos(2x), где x - угол, выраженный в радианах. Эта формула основана на тригонометрическом тождестве для удвоенного угла и является основой для ряда других математических преобразований.
Использование данной формулы позволяет значительно упростить решение многих задач, связанных с тригонометрическими функциями, а также облегчить вычисления при работе с углами. Понимание и умение применять эту формулу является важным элементом в подготовке и решении математических задач, требующих знания тригонометрии.
Как вычислить разность квадрата синуса и квадрата косинуса

Для вычисления разности квадрата синуса и квадрата косинуса можно воспользоваться формулой:
- Сначала найдите значение синуса и косинуса и возведите их в квадрат: sin^2(x) и cos^2(x).
- Вычислите разность sin^2(x) - cos^2(x).
- Используйте тригонометрические тождества, такие как sin^2(x) - cos^2(x) = 1 - cos(2x).
- Подставьте в полученное уравнение значение угла x для окончательного вычисления разности.
Формула разности синуса и косинуса

Sin^2(x) - Cos^2(x) = -tan^2(x)
Эта формула широко используется в тригонометрии и математике для упрощения выражений и решения различных задач.
Квадрат синуса и косинуса
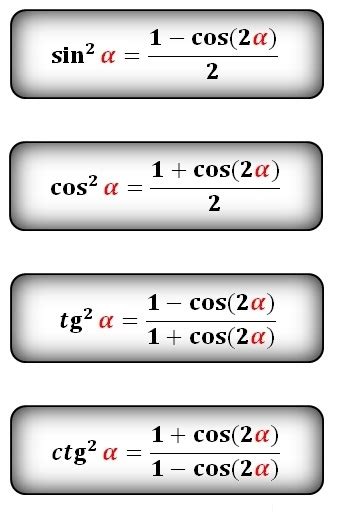
Формула разности:
sin^2(x) - cos^2(x) = 1
Это свойство тригонометрических функций можно использовать для упрощения выражений и решения уравнений. Например, зная данную формулу, можно легко найти значения синуса и косинуса при известном значении одной из функций.
Применение формулы

Данная формула может быть полезна при решении задач, связанных с тригонометрическими выражениями. Например, при вычислении интегралов с квадратами функций синуса и косинуса или при доказательстве тождеств в тригонометрии. Также она может применяться при решении уравнений, где встречаются квадраты тригонометрических функций.
Для наглядности и удобства использования данной формулы можно создать таблицу, в которой будут отображены все необходимые значения для вычисления разности квадрата синуса и квадрата косинуса.
| Угол | Синус угла | Косинус угла |
|---|---|---|
| α | sin(α) | cos(α) |
Расчеты с помощью формулы

Для вычисления разности квадрата синуса и квадрата косинуса можно воспользоваться следующей формулой:
$$\sin^2(x) - \cos^2(x) = \sin(x)^2 - \cos(x)^2 = -\cos(2x)$$
Эта формула позволяет эффективно вычислять разность квадратов синуса и косинуса для заданных значений угла x.
Математические аспекты в вычислениях

Математика играет важную роль во многих областях науки и техники, с их помощью мы можем описывать и анализировать различные явления. Вышеупомянутая формула для вычисления разности квадрата синуса и квадрата косинуса представляет собой математическое соотношение, которое применяется в тригонометрии.
Точное и правильное использование математических формул и выражений позволяют сильно упростить вычисления, предсказать различные прогностические величины и создавать новые математические модели для решения сложных задач. Математика - это универсальный язык, который позволяет точно и однозначно описывать различные процессы и зависимости.
- Математические формулы позволяют нам строить точные прогнозы и расчеты
- Использование математических методов позволяет сделать принципиально новые открытия
- Математика помогает строить сложные модели, описывающие закономерности в природе и обществе
Вопрос-ответ

Какая формула позволяет вычислить разность квадрата синуса и квадрата косинуса?
Формула для вычисления разности квадрата синуса и квадрата косинуса выглядит следующим образом: \( \sin^2(x) - \cos^2(x) = -\cos(2x) \). Это выражение получается из формулы двойного угла для косинуса.
Как можно использовать формулу для вычисления разности квадрата синуса и квадрата косинуса?
Формула \( \sin^2(x) - \cos^2(x) = -\cos(2x) \) часто используется при решении задач с тригонометрическими функциями. Например, она может быть полезна при интегрировании тригонометрических выражений или при доказательствах тождеств. Также эта формула может быть использована для упрощения сложных выражений с синусом и косинусом.



