Математическое моделирование является мощным инструментом, который позволяет описывать и анализировать разнообразные явления и процессы в природе, технике, экономике и других областях. Это процесс построения математических моделей, которые отражают основные характеристики изучаемого объекта и позволяют делать прогнозы, оптимизировать решения и проводить эксперименты в виртуальной среде.
Вычислительная математика – это область науки, которая занимается разработкой и применением численных методов и алгоритмов для решения математических задач с использованием компьютерных технологий. Современные методы численного анализа и компьютерные модели позволяют решать сложные задачи, которые невозможно решить аналитически, и проводить расчеты в реальном времени.
Взаимодействие математического моделирования и вычислительной математики позволяет создавать эффективные инструменты для анализа, прогнозирования и управления различными системами. Эта симбиоз позволяет решать широкий спектр задач, начиная от оптимизации производственных процессов и конструирования новых устройств, заканчивая исследованием климатических изменений и моделированием сложных социально-экономических систем.
Важность математического моделирования

Моделирование позволяет проводить виртуальные эксперименты, исследовать различные сценарии и оценивать их эффективность, что позволяет снизить затраты на реальные испытания и ускорить процесс разработки. Благодаря математическим моделям можно углубленно изучать сложные системы, понимать их внутреннее устройство и предсказывать их поведение.
Таким образом, математическое моделирование является мощным инструментом для выявления закономерностей, оптимизации процессов и принятия обоснованных решений на основе анализа данных. Оно играет важную роль в различных областях науки и техники, помогая оптимизировать деятельность и создавать новые технологии.
Значение математики в современном мире

Современные технологии и инновации неразрывно связаны с математикой. К примеру, разработка искусственного интеллекта, биоинформатика, криптография - все эти области нуждаются в математическом аппарате для своего развития. Математическое моделирование также находит применение в прогнозировании погоды, управлении финансами, оптимизации производственных процессов и многих других областях.
Таким образом, математика стала неотъемлемой частью современного мира и ее значение трудно переоценить. Знание математики открывает двери к широким возможностям для решения сложных задач и создания инноваций в различных областях человеческой деятельности.
Применение математических моделей

Математические модели широко используются в различных областях науки и техники. Они помогают предсказывать поведение сложных систем, исследовать закономерности процессов, оптимизировать параметры и принимать обоснованные решения. Применение математических моделей распространено в физике, химии, биологии, экономике, инженерии, медицине и других областях. Они позволяют анализировать данные, проводить численные эксперименты, предсказывать результаты, исследовать взаимосвязи между переменными и многое другое.
Основные этапы создания модели
1. Определение цели моделирования и формулирование задачи.
2. Сбор данных и информации, необходимых для построения модели.
3. Выбор метода моделирования и математических алгоритмов для решения задачи.
4. Построение математической модели на основе собранных данных.
5. Проверка и анализ модели на соответствие поставленной задаче.
6. Калибровка и верификация модели, сравнение результатов моделирования с реальными данными.
Выбор математических методов

При решении задач математического моделирования важно правильно выбирать математические методы. От выбора методов зависит точность и эффективность модели, а также время, затраченное на решение задачи.
Численные методы и аналитические методы являются основными подходами к решению математических задач. Численные методы используются для аппроксимации решения задачи, когда аналитическое решение невозможно или чрезвычайно сложно. Аналитические методы основаны на точной математической модели и позволяют получить точное аналитическое решение задачи.
Выбор между численными и аналитическими методами зависит от конкретной задачи, доступных ресурсов и требуемой точности решения. Нередко используется комбинация различных методов для достижения оптимальных результатов.
Построение математической модели
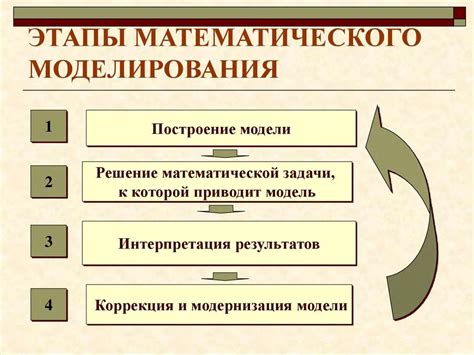
Одним из важных аспектов при построении математической модели является выбор подходящих переменных и параметров, которые будут участвовать в уравнениях модели. Эти переменные должны отражать ключевые характеристики системы и позволить точно предсказать ее поведение.
Роль вычислительной математики

Благодаря вычислительной математике можно проводить анализ данных, оптимизировать процессы, строить математические модели сложных систем, а также прогнозировать результаты экспериментов. Это позволяет экономить время и ресурсы, повышая эффективность и точность решения задач.
Одним из ключевых применений вычислительной математики является моделирование и симуляция физических, биологических, экономических и социальных процессов. Разработка новых численных методов и алгоритмов позволяет справляться с комплексными задачами и улучшить понимание основных закономерностей природы и общества.
Алгоритмы для решения математических задач
В области математического моделирования и вычислительной математики широко используются различные алгоритмы для решения разнообразных задач.
Один из самых популярных алгоритмов – метод наименьших квадратов, который применяется для поиска аппроксимирующих функций и минимизации ошибки при аппроксимации.
Другим важным алгоритмом является метод Гаусса-Зейделя, который используется для решения систем линейных уравнений методом последовательных итераций.
Также стоит упомянуть алгоритмы численного интегрирования, численного дифференцирования, алгоритмы поиска экстремумов функций и многие другие.
Выбор оптимального алгоритма зависит от конкретной задачи и требований к точности решения.
Вычислительные методы и их применение

Основные области применения вычислительных методов включают численное решение дифференциальных уравнений, аппроксимацию функций, оптимизацию параметров моделей, обработку и анализ данных, решение задач математической физики и многие другие.
Для реализации вычислительных методов широко используются программные средства, такие как языки программирования (например, Python, MATLAB), математические пакеты (например, NumPy, SciPy) и специализированные прикладные программы.
Применение вычислительных методов позволяет эффективно решать сложные задачи, обрабатывать большие объемы данных, проводить моделирование и анализ, что делает их неотъемлемой частью современной научной и инженерной деятельности.
| Область применения | Примеры методов |
|---|---|
| Математическое моделирование | Метод конечных разностей, метод конечных элементов |
| Обработка сигналов | Преобразование Фурье, фильтрация данных |
| Оптимизация | Генетические алгоритмы, методы оптимизации функций |
Вопрос-ответ

Что такое математическое моделирование и в чем заключаются его основные принципы?
Математическое моделирование - это процесс создания упрощенных математических описаний реальных систем с целью изучения их поведения и принятия решений. Основными принципами математического моделирования являются выбор соответствующей математической модели, ее параметризация, решение уравнений модели на компьютере и интерпретация полученных результатов.
Какие методы используют в вычислительной математике для решения сложных математических задач?
Вычислительная математика включает в себя различные методы решения математических задач, такие как численные методы (метод конечных разностей, метод конечных элементов) для решения дифференциальных уравнений, методы оптимизации (градиентный спуск, метод Ньютона) для поиска экстремумов функций, методы аппроксимации для приближенного представления функций и многие другие.
Каким образом математическое моделирование применяется в различных областях, например, в физике или экономике?
В различных областях науки математическое моделирование играет важную роль. В физике математические модели позволяют описывать поведение физических систем с высокой точностью. В экономике моделирование используется для прогнозирования экономических индикаторов и принятия решений о развитии рынков. В биологии моделирование помогает понять биологические процессы и воздействие различных факторов на живые организмы.



