Матрица – это упорядоченный набор чисел, организованных в виде таблицы. Она широко применяется в математике, физике, информатике и других областях науки.
Основное свойство матрицы – это ее размерность, представленная числом строк и столбцов. Матрицы могут быть квадратными, прямоугольными, нулевыми, единичными и так далее.
Определитель – это числовая характеристика квадратной матрицы, которая играет важную роль в линейной алгебре. Определитель матрицы позволяет определить, можно ли ту матрицу обратить или нет.
Матрица определителя: ключевые особенности и преимущества

Одним из ключевых преимуществ использования матрицы определителя является её эффективность при решении систем линейных уравнений. Определитель матрицы позволяет быстро определить, имеет ли система уравнений единственное решение, множество решений или не имеет решений вовсе.
| Преимущества матрицы определителя: |
| 1. Быстрое определение существования и единственности решения системы уравнений. |
| 2. Возможность выявления линейной зависимости между векторами и строками матрицы. |
| 3. Удобство при нахождении обратной матрицы. |
Определение и структура матрицы определителя

Структура матрицы определителя представляет собой квадратную таблицу, где элементы расположены по диагоналям, начиная с главной диагонали сверху вниз, а затем слева направо на дополнительные диагонали. Например, для матрицы 3x3 структура матрицы определителя будет следующей:
- Основная диагональ: элементы a11, a22, a33
- Первая дополнительная диагональ: элементы a12, a23, a31
- Вторая дополнительная диагональ: элементы a13, a21, a32
Элементы на диагоналях имеют положительные знаки, а элементы вне диагоналей имеют отрицательные знаки, образуя антисимметричную структуру.
Принцип работы и вычисление определителя

Для вычисления определителя матрицы существует несколько методов, включая метод миноров и метод преобразования строк. Один из самых широко применяемых методов для вычисления определителя – это метод разложения по строке (столбцу), когда определитель матрицы раскладывается на сумму произведений элементов и их миноров.
Итак, вычисление определителя матрицы – важная операция в линейной алгебре, которая позволяет оценить свойства матрицы и использовать ее в различных вычислениях и при решении систем линейных уравнений.
Основные различия между определителем и детерминантом

- Определитель матрицы - это число, которое может быть вычислено для квадратных матриц. Он представляет собой частный случай детерминанта. Детерминант же может быть найден для любой матрицы.
- Определитель обычно обозначается как |A| или det(A), в то время как детерминант матрицы A записывается как det(A).
- Определитель квадратной матрицы размером n*n будет иметь только одно значение, в то время как детерминант матрицы размером n*m может иметь различные значения в зависимости от размера матрицы.
- Определитель используется для решения линейных уравнений и нахождения площади параллелограмма, в то время как детерминант играет важную роль в теории линейной алгебры и вещественных функциях.
Таким образом, определитель и детерминант - это два важных понятия в математике, которые имеют свои уникальные особенности и применения.
Практическое применение матрицы определителя в математике

Для этого достаточно записать координаты векторов в виде матрицы и вычислить определитель этой матрицы. Абсолютное значение определителя будет равно площади параллелограмма, образованного указанными векторами.
Также матрица определителя используется для решения квадратных уравнений и систем линейных уравнений, а также при вычислении объемов многомерных фигур, векторных и тензорных операций.
Преимущества использования определителя в линейной алгебре

Для решения систем линейных уравнений и различных задач линейной алгебры часто используется определитель матрицы. Вот основные преимущества использования определителя:
| 1. | Позволяет быстро определить, является ли матрица обратимой (существует ли обратная матрица). |
| 2. | Используется для нахождения ранга матрицы и прямой суммы подпространств. |
| 3. | Позволяет вычислить объем n-мерного параллелепипеда, образованного векторами-столбцами матрицы. |
| 4. | Используется в формулах для вычисления собственных значений и собственных векторов. |
Использование определителя в линейной алгебре позволяет эффективно и компактно решать разнообразные задачи, связанные с матричными операциями и системами уравнений.
Примеры решения задач с использованием матрицы определителя
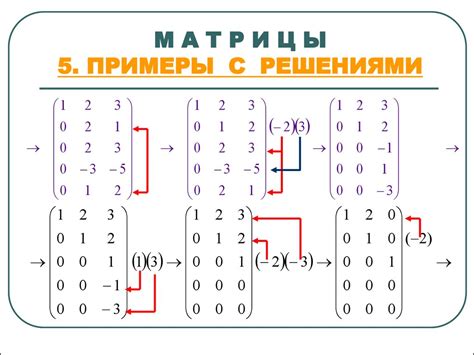
Для решения системы линейных уравнений можно использовать матрицы и их определители. Рассмотрим пример:
Система уравнений:
2x + 3y = 9
4x - y = 5
Запишем данную систему уравнений в матричной форме:
| 2 3 |
| 4 -1 |
Найдем определитель матрицы системы уравнений:
| 2 3 | * | 4 -1 | - | 3 3 | * | 2 -1 |
Определитель матрицы равен 2*(-1) - 3*4 = -11.
Таким образом, определитель не равен нулю, следовательно, система имеет единственное решение, которое можно найти с помощью метода Крамера.
Вопрос-ответ

Чем отличается матрица от определителя?
Матрица - это таблица чисел, упорядоченных по строкам и столбцам. Определитель - это число, вычисляемое по матрице и используемое для определения обратной матрицы и решения систем линейных уравнений.
Как вычисляется определитель матрицы?
Определитель матрицы вычисляется путем выполнения определенных операций с элементами матрицы. Например, для матрицы 2x2 определитель вычисляется как произведение элементов главной диагонали минус произведение элементов побочной диагонали.
Где применяется определитель матрицы в реальной жизни?
Определитель матрицы применяется для решения систем линейных уравнений, в теории вероятностей, при работе с векторами и координатами объектов в пространстве, в криптографии и других областях математики и информатики.
Какие ключевые свойства имеет определитель матрицы?
Определитель матрицы обладает такими свойствами как линейность, когда определитель суммы матриц равен сумме определителей матриц; мультипликативность, когда определитель произведения матриц равен произведению определителей матриц; и многие другие.
Какие отличия между матрицей и определителем?
Матрица - это таблица чисел, упорядоченных по строкам и столбцам, которая задает некоторый набор данных или операций. Определитель - это число, вычисляемое по матрице, которое является параметром, описывающим свойства матрицы, такие как линейная независимость строк или столбцов. Таким образом, матрица представляет набор чисел, а определитель используется для анализа свойств матрицы.



