Эллипс – это геометрическая фигура, которая образуется при пересечении плоскости и цилиндра. Эллипс имеет два фокуса и оси, которые являются его важными характеристиками.
Возникает вопрос о том, как можно найти эллипс в цилиндре? Для этого нужно задействовать специальные методы, например, проектирование или применение математических формул, учитывая свойства эллипса и цилиндра.
Признаки эллипса в цилиндре могут быть определены по его геометрическим характеристикам – радиусам и высоте цилиндра. Изучение данной фигуры позволяет решать задачи как в математике, так и в инженерных расчетах.
Эллипс в цилиндре: понятие и свойства
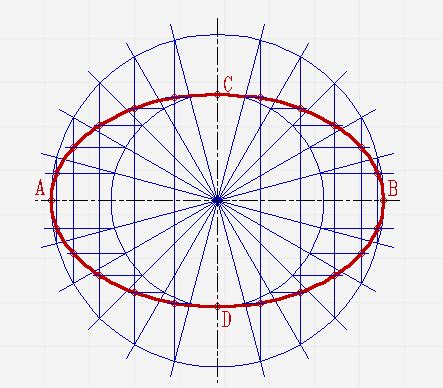
Свойства эллипса в цилиндре:
- Форма: Эллипс в цилиндре имеет форму замкнутого овала с двумя фокусами, расположенными на его главной оси.
- Размер: Размеры эллипса в цилиндре могут быть определены по полуосям и эксцентриситету.
- Фокусы: Фокусы эллипса в цилиндре являются точками, сумма расстояний от которых до любой точки на эллипсе одинакова.
- Фокусное расстояние: Расстояние между фокусами эллипса в цилиндре равно длине его главной оси.
- Дирекрисы: Дирекрисы эллипса в цилиндре - это прямые, проходящие через фокусы и перпендикулярные главной оси эллипса.
Определение и основные характеристики

В эллипсе есть два фокуса, расстояние между которыми является постоянной величиной и называется фокусным расстоянием. Также важным параметром эллипса является эксцентриситет, который характеризует его "овальность". Чем ближе эксцентриситет к нулю, тем более круглый эллипс, а при значении эксцентриситета равном единице эллипс превращается в параболу.
Методы поиска и анализа эллипсов
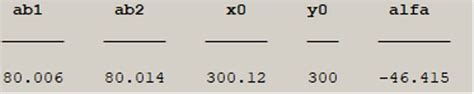
Существует несколько методов для поиска и анализа эллипсов в цилиндре. Они могут включать в себя следующие шаги:
| 1. | Использование математических уравнений для определения эллипса в цилиндре. |
| 2. | Метод определения фокусов эллипса и его основных параметров. |
| 3. | Анализ координат эллипса для определения его ориентации и формы. |
| 4. | Использование графических методов для визуализации и анализа эллипсов. |
Математические алгоритмы изучения эллипсов
Для исследования эллипсов также применяют методы аппроксимации и анализа точек, заданных на плоскости. Это позволяет оценить точность заданной формы эллипса и провести дальнейший анализ его свойств. Кроме того, существуют специальные алгоритмы для построения эллипсов по заданным параметрам, что позволяет создавать и моделировать различные геометрические объекты.
Признаки эллипса в цилиндре
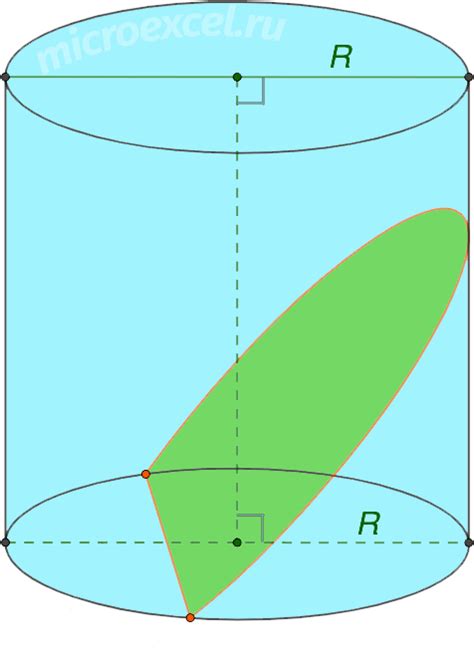
Эллипс в цилиндре обладает рядом характерных признаков, которые помогают определить его среди других фигур:
- Форма: эллипс в цилиндре представляет собой кривую замкнутую фигуру, которая напоминает форму яйца или овала.
- Две фокуса: любая точка на эллипсе в цилиндре является суммой расстояний до двух фокусов, расположенных на оси.
- Больший и малый радиус: эллипс в цилиндре имеет два радиуса – большой (от центра до наиболее удаленной точки) и малый (от центра до наиболее близкой точки).
- Симметрия: эллипс в цилиндре является фигурой с двумя осиальными симметриями, проходящими через его центр и фокусы.
- Уравнение: уравнение эллипса в цилиндре имеет вид x^2/a^2 + y^2/b^2 = 1, где a и b – полуоси эллипса.
Отличительные особенности эллипсов

- Форма: эллипс может быть вытянут в вертикальном или горизонтальном направлении, что определяется соотношением длин осей.
- Оси: эллипс имеет две оси – большую (главную) и меньшую (второстепенную).
- Фокусы: эллипс определяется двумя фокусами, сумма расстояний до которых от любой точки эллипса постоянна.
- Эксцентриситет: это параметр, характеризующий степень вытянутости эллипса. Для круга эксцентриситет равен нулю, а для вытянутого эллипса он больше нуля и меньше единицы.
Вопрос-ответ

Что такое эллипс в цилиндре?
Эллипс в цилиндре - это плоская замкнутая кривая, которая представляет собой пересечение плоскости и цилиндра. Эллипс имеет две оси симметрии и обладает особыми свойствами, такими как фокусы, полуоси, эксцентриситет и другие.
Какие методы используются для определения эллипса в цилиндре?
Для определения эллипса в цилиндре можно использовать ряд методов. Один из них - метод пересечения плоскости и цилиндра с последующим анализом уравнений этого пересечения. Также можно использовать метод проекций, при котором проецируется эллипс на плоскость.
Какие признаки имеет эллипс в цилиндре?
Эллипс в цилиндре имеет ряд характеристических признаков, таких как симметрия относительно осей, наличие фокусов, равенство суммы расстояний от фокусов до точки эллипса. Также эллипс обладает особым свойством касания к цилиндру в двух точках.



