В тригонометрии одно из важнейших понятий – знак выражения, которое задает функция. Знание о знаке выражения позволяет определить, в каких квадрантах плоскости оно будет положительным или отрицательным. Для этого необходимо рассмотреть значения функции на основных углах и использовать правила интервалов.
В математике знак числа не всегда определен только через его алгебраическое значение. В тригонометрии дополнительно учитывается расположение точки на плоскости относительно начальной точки координат – точки (0, 0). Положительные значения функции (синус, косинус, тангенс и др.) соответствуют углам, лежащим в определенных квадрантах, а отрицательные – в остальных.
Важно отметить, что знание знака выражения позволяет более точно анализировать графики функций, находить корни уравнений, а также решать разнообразные тригонометрические задачи.
Понятие и основы:

Для определения знака выражения в тригонометрии необходимо учитывать четверть, в которой находится угол, а также знаки функций синуса, косинуса и тангенса. В зависимости от знаков этих функций и четверти, в которой находится угол, определяется знак выражения.
Для подробного определения знака выражения в тригонометрии используется таблица знаков углов в различных четвертях плоскости:
| Четверть плоскости | Знаки sin, cos, tg |
|---|---|
| I | + |
| II | - |
| III | - |
| IV | + |
Как определить знак выражения в тригонометрии?

Также важно запомнить знаки функций в особых точках: 0, π/2, π, 3π/2. Для синуса верно: sin(0) = 0, sin(π/2) = 1, sin(π) = 0, sin(3π/2) = -1. Для косинуса: cos(0) = 1, cos(π/2) = 0, cos(π) = -1, cos(3π/2) = 0.
При работе с выражениями в тригонометрии, важно учитывать знак каждой функции и правильно их сочетать, чтобы определить знак всего выражения.
Тригонометрические функции:
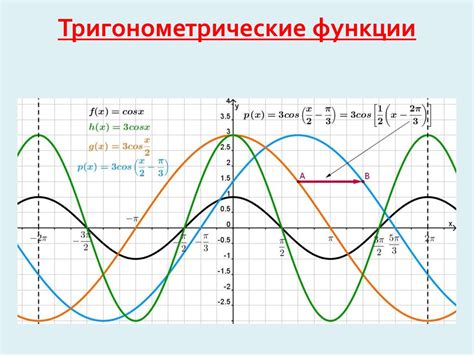
| Функция | Обозначение |
|---|---|
| Синус | sin |
| Косинус | cos |
| Тангенс | tan |
| Котангенс | cot |
| Секанс | sec |
| Косеканс | csc |
Эти функции широко применяются в математике, физике, инженерии и других науках для анализа и решения задач, связанных с углами и векторами.
Функции Sin, Cos, Tan в тригонометрии

Функции синуса (sin), косинуса (cos) и тангенса (tan) широко используются в математике и физике для описания зависимостей между углами и длиной сторон прямоугольного треугольника.
Синус (sin) угла в прямоугольном треугольнике определяется отношением противолежащего катета к гипотенузе.
Косинус (cos) угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе.
Тангенс (tan) угла в прямоугольном треугольнике вычисляется как отношение противолежащего катета к прилежащему катету.
Зависимость от угла:

Для определения знака выражения необходимо учитывать квадрант, в который попадает угол. В первом квадранте все тригонометрические функции положительны, во втором - синус и тангенс, в третьем - тангенс и котангенс, в четвертом - косинус и котангенс.
Изменение знака при углах

В тригонометрии знак тригонометрических функций синуса, косинуса и тангенса зависит от значения угла в соответствующей четверти координатной плоскости.
1. I четверть: В I четверти все тригонометрические функции положительны: sin θ > 0, cos θ > 0, tg θ > 0.
2. II четверть: В II четверти sin θ > 0, cos θ < 0, tg θ < 0.
3. III четверть: В III четверти sin θ < 0, cos θ < 0, tg θ > 0.
4. IV четверть: В IV четверти sin θ < 0, cos θ > 0, tg θ < 0.
Изменение знака функций при различных углах необходимо учитывать при решении тригонометрических уравнений и задач.
Решение уравнений:

Для определения знака выражения в тригонометрии и решения уравнений необходимо:
- Разложить уравнение на элементарные составляющие.
- Применить формулы тригонометрии для упрощения выражения.
- Решить полученное уравнение, учитывая значения угловых функций для конкретных углов.
После проведения вышеперечисленных шагов можно определить знак выражения в зависимости от решения уравнения и значений угловых функций.
Нахождение знака при решении

При решении задач в тригонометрии можно определить знак выражения, используя знаки функций в соответствующих квадрантах угла.
| 1 квадрант | Все функции тригонометрии положительны: sin, cos, tg, ctg, sec, cosec. |
| 2 квадрант | Только sin и cosec функции положительны. |
| 3 квадрант | Только tg и ctg функции положительны. |
| 4 квадрант | Только cos и sec функции положительны. |
Полезные формулы:

1. Знак синуса угла в разных четвертях координатной плоскости:
- В первой четверти: sin(α) > 0
- Во второй четверти: sin(α) > 0
- В третьей четверти: sin(α) < 0
- В четвертой четверти: sin(α) < 0
2. Знак косинуса угла в разных четвертях координатной плоскости:
- В первой четверти: cos(α) > 0
- Во второй четверти: cos(α) < 0
- В третьей четверти: cos(α) < 0
- В четвертой четверти: cos(α) > 0
3. Знак тангенса угла в разных четвертях координатной плоскости:
- В первой четверти: tg(α) > 0
- Во второй четверти: tg(α) < 0
- В третьей четверти: tg(α) > 0
- В четвертой четверти: tg(α) < 0
Вопрос-ответ

Что такое определение знака выражения в тригонометрии?
Определение знака выражения в тригонометрии связано с определением знаков функций синуса, косинуса и тангенса в различных четвертях плоскости. В зависимости от знаков углов, выражения могут быть положительными или отрицательными.
Как определить знак выражения с тригонометрическими функциями?
Для определения знака выражения с тригонометрическими функциями необходимо анализировать величины углов, на которых заданы эти функции. Исходя из положения угла относительно осей координат, можно определить знак функций синуса, косинуса и тангенса.
Почему важно знать знаки тригонометрических функций?
Знание знаков тригонометрических функций помогает не только определять знак выражений при решении уравнений и неравенств, но и понимать геометрический смысл углов и тригонометрических функций в различных четвертях плоскости.
Какие методы можно использовать для определения знака выражения в тригонометрии?
Для определения знака выражения в тригонометрии можно использовать анализ геометрического расположения углов и тригонометрических функций, а также применять правила по знакам функций в различных четвертях плоскости.
Каково значение знака тригонометрических функций в первой четверти?
В первой четверти углы принимают значения от 0 до π/2, при этом синус и тангенс положительны, а косинус равен 1. Таким образом, в первой четверти тригонометрические функции могут быть положительными.



