Определитель второго порядка в матрице - это важное понятие в линейной алгебре, которое позволяет определить свойства и характеристики матрицы. Определитель матрицы размером 2x2 вычисляется по определённой формуле и является числовой характеристикой.
Существует несколько методов для вычисления определителя второго порядка, включая формулу с использованием элементов матрицы и геометрическое представление через площадь параллелограмма, образованного векторами, представленными столбцами матрицы.
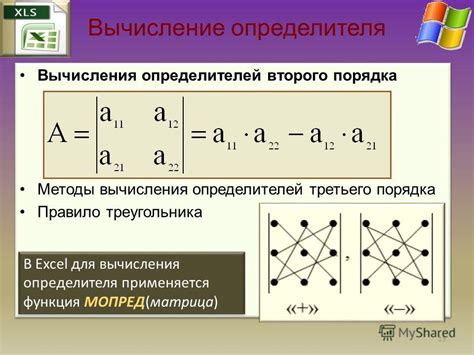
Примером вычисления определителя 2x2 матрицы является следующая операция: при заданных элементах матрицы а11, а12, а21, а22 необходимо умножить элементы главной диагонали (а11 * а22) и элементы побочной диагонали (а12 * а21), а затем вычесть полученные произведения друг из друга. Таким образом, определитель даст числовое значение, характеризующее матрицу.
Определитель второго порядка в матрице

A = | a b |
| c d |
определитель второго порядка равен произведению элементов главной диагонали минус произведению элементов побочной диагонали:
det(A) = a*d - b*c
Например, для матрицы A = | 2 4 |
| 1 3 |
определитель равен 2*3 - 4*1 = 6 - 4 = 2.
Понятие, суть и определение

Для квадратной матрицы размером 2х2 определитель вычисляется по формуле:
| det(A) = | | a b | |
| | c d | |
где a, b, c, d - элементы матрицы. Определитель вычисляется как произведение элемента a на элемент d минус произведение элемента b на элемент c.
Таким образом, определитель второго порядка в матрице позволяет определить, является ли матрица невырожденной (если det(A) ≠ 0) или вырожденной (если det(A) = 0).
Методы вычисления определителя
Существует несколько методов вычисления определителя матрицы:
| 1. Метод миноров и алгебраических дополнений: | Данный метод основан на представлении определителя как суммы произведений элементов матрицы на их алгебраические дополнения. |
| 2. Метод построчного разложения: | Определитель можно вычислить, разложив его по любой строке (или столбцу) матрицы на сумму произведений элементов строки (столбца) на определители полученных миноров. |
| 3. Метод элементарных преобразований: | Определитель не изменяется, если к любой строке (столбцу) матрицы прибавить (вычесть) её линейную комбинацию с другими строками (столбцами). |
Выбор метода вычисления определителя зависит от конкретной задачи и математических удобств.
Примеры применения определителя второго порядка

Определитель второго порядка широко используется в линейной алгебре и математическом анализе для решения систем линейных уравнений и определения обратной матрицы.
Примеры применения второго порядка:
- Расчет площади параллелограмма, построенного на векторах.
- Решение системы двух линейных уравнений с двумя неизвестными.
- Нахождение обратной матрицы при помощи формулы 1/|A|*adj(A), где A - исходная матрица, |A| - определитель, adj(A) - алгебраическое дополнение.
- Определение невырожденности матрицы и ее ранга.
Значение определителя в алгебре

Одним из ключевых свойств определителя является возможность определить, обратима ли матрица. Если определитель матрицы не равен нулю, то матрица называется обратимой.
Определитель также играет важную роль при решении систем линейных уравнений. Он может определить существование, единственность и разрешимость решения системы.
Свойства определителя второго порядка

Определитель второго порядка матрицы 2x2 вычисляется как произведение главной диагонали минус произведение побочной диагонали.
Свойство 1: Если определитель равен нулю, то матрица вырожденная, т.е. у нее нет обратной матрицы.
Свойство 2: При умножении всех элементов строки или столбца матрицы на число, определитель тоже умножается на это число.
Свойство 3: При перестановке двух строк или двух столбцов определитель меняет знак.
Практическое применение в задачах

Определитель второго порядка в матрице полезен в различных областях, таких как аналитическая геометрия, физика, экономика и многие другие. Например, определитель матрицы может применяться для решения систем линейных уравнений, вычисления площади параллелограмма или объема пирамиды, определения невырожденности матрицы и многих других задач.
При работе с линейными уравнениями определитель матрицы используется для определения существования и единственности решения системы уравнений. В физике он может применяться для анализа различных законов и закономерностей.
Также определитель матрицы играет ключевую роль в линейной алгебре и теории групп, где он используется для рассмотрения свойств линейных преобразований и решении задач линейной оптимизации.
Решение уравнений с помощью определителя

Для решения систем линейных уравнений можно использовать метод Крамера, который основан на определителе матрицы коэффициентов.
Пусть дана система уравнений:
Ax = b
где A - матрица коэффициентов, x - вектор-столбец неизвестных, b - вектор-столбец свободных членов.
Для решения уравнения найдем определитель матрицы коэффициентов (detA). Если определитель не равен нулю, система имеет единственное решение, которое можно найти по формулам:
xi = detAi / detA, где detAi - определитель, полученный заменой i-го столбца вектором b.
Этот метод позволяет находить решение систем уравнений с помощью определителя и обеспечивает высокую точность результатов. Однако он ограничен размером системы и требует обращения матрицы, что может быть затратным с точки зрения вычислений.
Вопрос-ответ

Что такое определитель второго порядка в матрице?
Определитель второго порядка в матрице - это число, которое вычисляется для матрицы 2x2 и используется для характеризации этой матрицы. Он обозначается символом det и вычисляется по формуле: det(A) = a*d - b*c, где матрица A = [[a, b], [c, d]].
Как вычислить определитель второго порядка в матрице?
Для вычисления определителя второго порядка в матрице 2x2 необходимо перемножить диагональные элементы матрицы и вычесть произведение второй диагонали. Например, для матрицы A = [[2, 1], [3, 4]] определитель вычисляется по формуле det(A) = 2*4 - 1*3 = 8 - 3 = 5.



