Отрезок – это часть прямой, ограниченная двумя точками. В алгебре, понимание понятия отрезка является одним из основополагающих элементов, который используется при решении различных задач и уравнений.
Отрезок характеризуется своими геометрическими и алгебраическими свойствами. Одним из важных свойств отрезка является его длина, которая измеряется величиной между двумя конечными точками отрезка.
При работе с отрезками в алгебре 7 класса важно уметь правильно определять их длину, а также учитывать свойства и особенности в рамках задач и упражнений. В данной статье мы рассмотрим основные понятия, свойства и примеры отрезков в алгебре.
Отрезок в алгебре 7 класс
Свойства отрезка:
1. Длина отрезка - расстояние между его концами. Она равна модулю разности координат концов отрезка на числовой прямой.
2. Отрезок имеет направление и указывается от одного конца к другому.
Пример:
Дан отрезок AB на числовой прямой. Координаты точек A и B: A(-3) и B(5). Длина отрезка AB равна |5 - (-3)| = |5 + 3| = 8.
Определение отрезка в алгебре

Свойства отрезка в алгебре 7 класс

Отрезок в алгебре обладает следующими основными свойствами:
| 1. Длина отрезка | Длина отрезка - это расстояние между его конечными точками. Она может быть выражена числом и является величиной безразмерной. |
| 2. Середина отрезка | Середина отрезка - это точка, которая делит отрезок на две равные части. Координаты середины отрезка можно найти, используя формулы средней пропорциональности. |
| 3. Четырехугольник | Отрезок можно рассматривать как сторону четырехугольника. Добавление отрезков и выполнение операций с ними может использоваться для нахождения периметра и площади четырехугольника. |
Отрезок в алгебре: геометрическая интерпретация
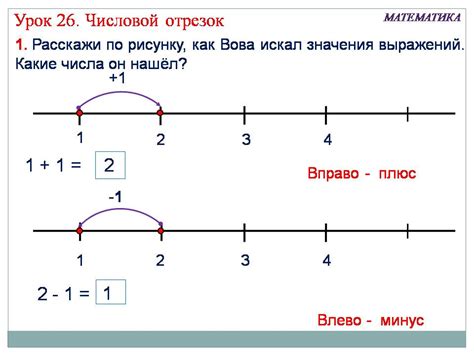
Отрезок в алгебре представляет собой часть прямой, ограниченную двумя точками. Геометрически отрезок можно представить как отрезок прямой линии между двумя точками. Эти точки называются концами отрезка.
Визуализация отрезка может помочь понять его свойства и использование при решении задач. На рисунке ниже приведен пример отрезка AB, обозначенного двумя точками A и B:
| A | ––– | B |
Главное свойство отрезка – его длина, которая равна расстоянию между его концами. Отрезок также имеет направление: можно указать начало и конец отрезка, что иногда важно при решении задач. Зная длину отрезка и его направление, можно проводить различные операции, например, находить среднюю точку отрезка или делить его на равные части.
Примеры использования отрезка в алгебре:
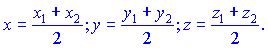
2. Рассмотрим отрезок CD, длина которого равна 5. Если точка C имеет координату 3, найдем координату точки D: D = C + |CD| = 3 + 5 = 8.
3. Для отрезка EF известно, что его середина находится в точке M с координатами 7. Найдем координаты концов отрезка E и F: E = M - |ME| = 7 - 3 = 4, F = M + |MF| = 7 + 3 = 10.
Отрезок в алгебре: основные формулы
Длина отрезка AB вычисляется по формуле:
AB = |a - b|, где a и b – координаты точек A и B соответственно.
Координаты середины отрезка AB находятся по формуле:
M(x, y) = ((x1 + x2) / 2, (y1 + y2) / 2), где (x1, y1) и (x2, y2) – координаты точек A и B.
Практическое применение отрезка в алгебре
| 1. | Геометрия. Отрезки используются для построения фигур, расчетов площадей и объемов, решения задач на расстояние между точками и многое другое. |
| 2. | Физика. Отрезки могут использоваться для моделирования движения тел, определения их скоростей и ускорений, а также для анализа сил и энергии в системах. |
| 3. | Информатика. Отрезки могут быть представлены как интервалы чисел в программировании для решения задач на сортировку, поиск и другие алгоритмы. |
| 4. | Экономика. В экономических моделях отрезки могут использоваться для оценки временных интервалов, расчета доходов и расходов, анализа рынков и т.д. |
Вопрос-ответ

Что такое отрезок в алгебре?
В алгебре отрезок - это участок прямой, ограниченный двумя точками. Он представляет собой конечный отрезок прямой, который можно измерить величиной (длиной). Отрезок обозначается двумя точками (A B) и содержит все точки прямой между этими двумя точками и эти точки сами (A и B).
Какие свойства отрезков в алгебре?
Отрезок является ограниченной частью прямой, поэтому на нем выполняются следующие свойства: сумма длин двух отрезков, образующих больший отрезок, равна длине этого большего отрезка; отрезок равный самому себе; отрезок, который может быть помещен в другой отрезок не превосходя по длине, равен величине этого отрезка.
Можете привести примеры отрезков в алгебре?
Конкретные примеры отрезков в алгебре могут быть отрезок между точками A(-3) и B(4), отрезок между точками C(0) и D(6), или отрезок между точками E(2) и F(2). Эти отрезки можно измерить по длине и определить их положение на числовой прямой.



