Квадратный корень - это математическая операция, которая отражает величину числа, которая при умножении на себя дает изначальное число. На первый взгляд может показаться, что квадратные корни имеют мало практического значения в повседневной жизни, однако на самом деле они широко применяются в различных сферах деятельности.
Например, в финансовой сфере квадратные корни используются для расчета волатильности акций или рисков инвестиций. Архитекторы и дизайнеры часто применяют квадратные корни для расчета пропорций и размеров строений, мебели и объектов искусства. В технических областях, таких как физика и инженерия, квадратные корни играют важную роль при решении задач и разработке новых технологий.
Умение правильно использовать квадратные корни позволяет улучшить качество принимаемых решений, повысить точность вычислений и предсказаний, а также расширить свой кругозор в различных областях знаний.
Квадратный корень: как применять в повседневной жизни

Вот несколько способов, как можно применить квадратный корень в повседневной жизни:
- Расчет площади квадратного участка земли. Если известна длина стороны квадрата, чтобы узнать его площадь, нужно вычислить квадратный корень из площади.
- Расчет скорости движения. Например, если известно расстояние и время движения, то можно вычислить скорость, взяв квадратный корень из отношения пройденного расстояния к времени.
- Оценка затрат времени или денег. При планировании задач или расходов можно использовать квадратный корень как инструмент для оценки времени выполнения или финансовых затрат.
Таким образом, знание квадратного корня может пригодиться в различных ситуациях, помогая быстро решать задачи и делать правильные расчеты в повседневной жизни.
Вычисление площадей и периметров
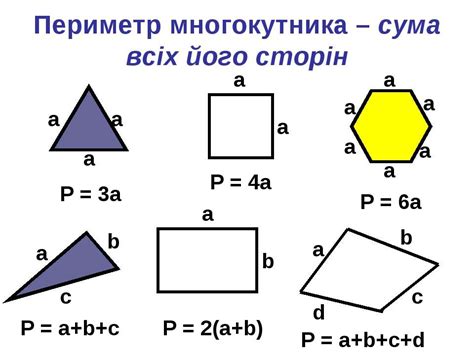
Квадратный корень часто используется для вычисления площадей и периметров различных фигур. Например, чтобы найти сторону квадрата по его площади, нужно извлечь квадратный корень из этой площади. Аналогично, чтобы найти длину стороны прямоугольника по заданной площади и ширине, можно воспользоваться квадратным корнем. Также, когда известен периметр квадрата или прямоугольника, квадратный корень позволит найти длину стороны.
Для более сложных фигур, таких как круг, квадратный корень используется для вычисления длины радиуса по известной площади или чтобы найти длину диаметра. Таким образом, знание квадратного корня может быть полезным при работе с геометрическими задачами и решении повседневных задач, связанных с площадями и периметрами различных фигур.
Оценка расстояний и глубины
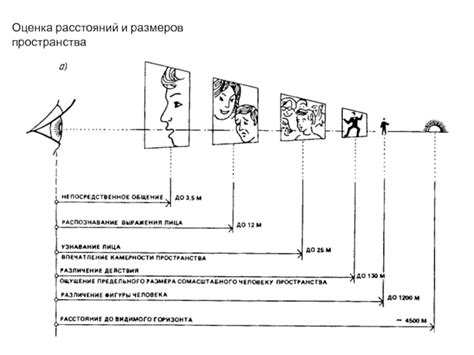
Квадратный корень используется для оценки расстояний и глубины в различных сферах жизни. Например, при измерении расстояний между двумя точками на карте или в реальном мире, квадратный корень помогает нам вычислить точное значение расстояния. Также при определении глубины озера или моря, квадратный корень может быть использован для оценки этого параметра.
Для примера, если нам известно, что глубина озера равна квадрату числа 25 метров (25² = 625), то чтобы найти глубину озера, нам нужно извлечь квадратный корень из 625, что равно 25 метров. Таким образом, квадратный корень позволяет нам быстро и точно оценить расстояния и глубины в повседневной жизни.
Расчет времени падения тела

Квадратный корень часто используется для расчетов времени падения тела. Физический закон свободного падения утверждает, что время, за которое тело падает на определенное расстояние, зависит от высоты, с которой оно выпускается. Формула для расчета времени падения:
- Вычислить высоту с падения.
- Использовать формулу времени падения: $$ t = \sqrt{\frac{2h}{g}} $$
- Где $$ h $$ - высота с падения, $$ g $$ - ускорение свободного падения (примерно 9.8 м/с2 на Земле).
- Подставить значения и вычислить квадратный корень из полученного выражения, чтобы найти время падения тела.
Прогнозирование погоды и температуры
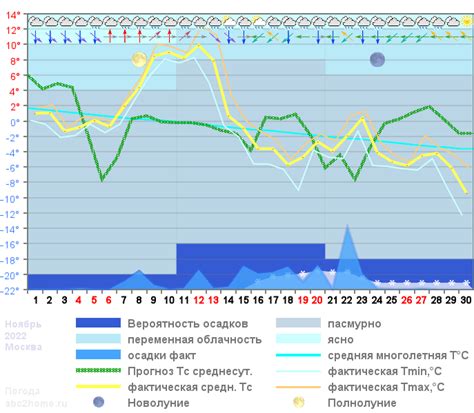
Например, когда анализируются температурные показатели за определенный период времени, квадратный корень может быть использован для оценки средней температуры или изменений в температуре в течение дня. Такие вычисления позволяют метеорологам более точно прогнозировать погодные явления и предсказывать изменения температуры в будущем.
| Пример | Квадратный корень |
|---|---|
| Средняя температура за день | √(T1 + T2 + T3 + ... + Tn) / n |
| Прогноз изменения температуры | √(Tn - Tn-1) |
Оценка потребления калорий и питательных веществ

Когда мы составляем рацион питания, важно учитывать количество потребляемых калорий и питательных веществ. Квадратный корень может помочь нам в оценке этого процесса. Например, если мы знаем общее количество калорий, потребляемых за день, мы можем рассчитать среднее количество калорий, употребляемых в каждом приеме пищи, используя квадратный корень.
Также, квадратный корень может быть применен для оценки среднего содержания определенного питательного вещества в продуктах. Например, если нам нужно узнать среднее содержание витамина С в различных фруктах, можно взять квадратный корень из суммы содержания витамина С в каждом фрукте.
Таким образом, применение квадратного корня в оценке потребления калорий и питательных веществ позволяет нам более осознанно подходить к составлению здорового и сбалансированного рациона питания.
Изучение физики и математики

Знание квадратного корня позволяет решать задачи из различных областей, таких как физика, экономика, инженерное дело и другие. Например, при изучении физики, квадратный корень используется для расчета скорости, ускорения, расстояний и других величин.
Понимание математических принципов и умение решать задачи с использованием квадратного корня помогает студентам развивать логическое мышление, аналитические навыки и способность применять знания в практических ситуациях.
Разработка компьютерных программ и алгоритмов

Квадратный корень часто используется в различных алгоритмах и программных решениях. Например, при разработке программ для инженерных расчетов, квадратный корень позволяет вычислять длину вектора, дистанцию между точками, а также использовать его в математических функциях для оптимизации работы программы. Кроме того, в алгоритмах машинного обучения и обработки изображений применение квадратного корня может быть необходимо для нормализации данных или вычисления расстояний между объектами. Эффективное использование квадратного корня может значительно повысить производительность программы и качество ее работы.
Улучшение навыков в бизнесе и финансах

Например, при анализе финансовой отчетности предприятия, можно использовать квадратный корень для расчета стандартного отклонения, коэффициента вариации или других показателей, которые помогут понять состояние компании и принять обоснованные решения.
Также, при оценке рисков в финансовых операциях, квадратный корень может использоваться для расчета волатильности ценных бумаг или определения вероятности возникновения неблагоприятных ситуаций.
Поэтому, развитие навыков работы с квадратным корнем в контексте бизнеса и финансов может существенно повысить профессиональный уровень и помочь принимать более обоснованные решения в сложных ситуациях.
Вопрос-ответ

Зачем нужно знать квадратный корень в повседневной жизни?
Знание квадратного корня может быть полезным при решении задач связанных с измерением площади комнаты, расчетом длины стороны квадрата, определением времени падения предмета и других повседневных ситуациях обращения с числами.
Как можно использовать квадратный корень при планировании строительства дома?
При планировании строительства дома, квадратный корень может помочь в расчетах площади помещений, определении необходимого количества строительных материалов, а также при оценке прочности конструкций.
Какие бытовые задачи можно решить, зная квадратный корень?
Зная квадратный корень, вы сможете быстро оценить округлую площадь ковра или обоев, узнать длину стороны квадрата по его площади, а также рассчитать среднее время нахождения на работе, чтобы планировать расходы времени.
Как выглядит пример решения задачи с использованием квадратного корня в бытовой ситуации?
Например, если у вас есть ковер площадью 16 квадратных метров, чтобы узнать его длину в метрах, нужно взять квадратный корень из 16, что равно 4 метрам. Таким образом, длина стороны ковра составляет 4 метра.



