Прямоугольный треугольник - это геометрическая фигура со свойствами, которые можно изучать и познавать. Один из углов в таком треугольнике обычно равен 90 градусов, но что делает углы в оставшихся вершинах равными?
Угол в 30 градусов в прямоугольном треугольнике может возникнуть в результате применения теоремы синусов или косинусов в сочетании с правильным выбором сторон треугольника. Интересно, какие именно условия позволяют определить такой угол?
Изучив теорию и решив несколько упражнений, можно убедиться в том, что угол в 30 градусов в прямоугольном треугольнике оказывается возможным и законным все благодаря математике и геометрии.
Геометрические свойства угла 30 градусов
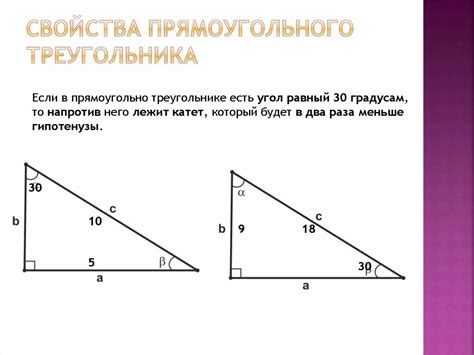
Угол в прямоугольном треугольнике

Угол в прямоугольном треугольнике может быть равен 30 градусов, если один из катетов равен 1, а другой катет равен √3. В таком случае, по определению тригонометрических функций, синус угла равен 1/2, что соответствует углу 30 градусов.
Также, угол в прямоугольном треугольнике может быть равен 30 градусов, если это угол между катетами соответственно 1 и 2. В этом случае, применяя теорему Пифагора, мы получаем, что гипотенуза треугольника равна корню из \(1^2 + 2^2 = 5\), и значит синус угла равен 2/√5, что также соответствует углу 30 градусов.
Возможность соответствующих сторон
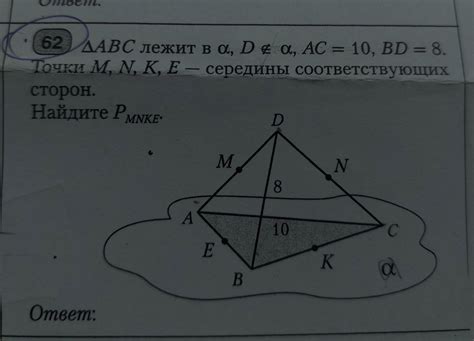
Такое соотношение сторон возможно, если угол прямоугольного треугольника равен 30 градусов.
Вопрос-ответ

Почему в прямоугольном треугольнике угол может быть равен 30 градусов?
Угол в прямоугольном треугольнике может быть равен 30 градусов, если он является углом противоположным кратной стороне меньшей длины в отношении 1:2. Такой треугольник называется равнобедренным прямоугольным треугольником. Угол в 30 градусов возникает из того, что в нем сторона, против которой он находится, равна половине стороны, к которой он примыкает.
Как можно обосновать равенство угла в 30 градусов в прямоугольном треугольнике?
Равенство угла в 30 градусов в прямоугольном треугольнике может быть обосновано с помощью геометрических свойств. Например, если взять равнобедренный прямоугольный треугольник со сторонами в отношении 2:1, то угол, противолежащий кратной стороне, будет равен 30 градусов. Это следует из свойств треугольника и особенностей геометрии углов прямоугольного треугольника.
Какой смысл имеет угол 30 градусов в равнобедренном прямоугольном треугольнике?
Угол в 30 градусов в равнобедренном прямоугольном треугольнике является специальным углом и имеет свои геометрические особенности. Он соответствует отношению сторон в 1:2 и помогает определять первичные геометрические соотношения в треугольнике. Этот угол также важен при решении геометрических задач и вычислении смежных углов.



