Область определения функции - это множество всех возможных входных значений, для которых функция определена. В математике область определения функции помогает определить, какие значения аргумента могут быть подставлены в функцию и какие значения функции можно получить при этом.
Например, если у нас есть функция f(x) = √x (корень из x), то область определения этой функции - все неотрицательные числа, т.е. x >= 0. Поскольку нельзя извлечь корень из отрицательного числа.
Область определения играет важную роль в математике, поскольку она помогает избежать ошибок при работе с функциями и определять их поведение при различных входных данных.
Понятие области определения

Например, функция f(x) = 1/x имеет область определения всех действительных чисел, за исключением x = 0, так как деление на ноль не определено. Таким образом, областью определения этой функции является множество всех действительных чисел, кроме нуля.
Знание области определения функции важно при решении уравнений, нахождении асимптот, определении области значений и других аспектах работы с функциями.
Определение и основные характеристики

Основные характеристики области определения функции включают в себя:
- Интервалы: Область определения может быть задана с помощью интервалов на числовой прямой, например, отрезки [a, b], полуинтервалы [a, b) или (a, b], или же интервалы (a, b).
- Условия: Иногда область определения может быть ограничена определенными условиями, например, функции с аргументом в знаменателе, где аргумент не может быть равен нулю.
Значения функции и область определения
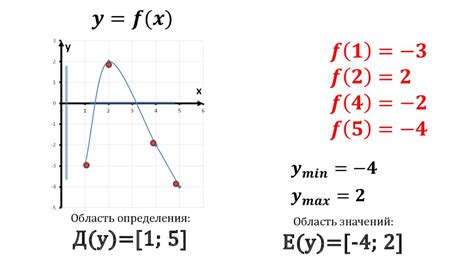
Значения функции - это результаты, получаемые при подстановке элементов области определения в функцию. То есть, значения функции - это множество всех возможных выходных значений, которые функция принимает для соответствующих входных значений.
Пример: для функции f(x) = x^2, область определения - множество всех действительных чисел, а значения функции - множество всех неотрицательных чисел, так как квадрат любого числа всегда неотрицателен.
Связь между значениями и областью определения

Значение функции зависит от области определения, в которой функция задана. Область определения функции определяет, на каких значениях аргумента функция может быть вычислена. Если значение аргумента находится за пределами области определения, то функция не определена и не имеет конкретного значения на этом аргументе.
Например, для функции f(x) = √x, область определения состоит из неотрицательных чисел, так как корень из отрицательного числа не определен в действительных числах.
Если попытаться вычислить f(-1), то функция не будет определена, так как -1 не принадлежит области определения функции √x.
Примеры области определения

1. Функция f(x) = √x имеет область определения D = [0, +∞), так как корень из отрицательного числа не существует.
2. Для функции g(x) = 1/x область определения D = x ≠ 0, так как деление на ноль невозможно.
3. Функция h(x) = log(x) определена для x > 0, поэтому ее область определения D = (0, +∞).
Иллюстрации на конкретных функциях

Для лучшего понимания области определения функций, рассмотрим несколько конкретных примеров:
- Функция f(x) = x^2:
- Функция g(x) = 1/x:
- Функция h(x) = √x:
Эта функция определена для всех вещественных чисел x, так как квадрат любого числа – неотрицательное число, и парабола графика функции будет протягиваться на всей числовой прямой.
Данная функция не определена при x = 0, так как деление на ноль невозможно. Значит, область определения функции g(x) – множество всех вещественных чисел, кроме нуля.
Функция корня определена только для неотрицательных чисел, так как извлечение корня из отрицательного числа приводит к мнимым числам. Следовательно, область определения функции h(x) – все неотрицательные числа (включая ноль).
Вопрос-ответ

Что такое область определения в математике?
Область определения функции - это множество всех значений, для которых функция определена. То есть, это все значения аргумента, при которых функция имеет смысл и может вычисляться.
Как можно определить область определения функции?
Область определения функции определяется условиями, при которых функция является корректно определенной. Например, для функции вида f(x) = 1/x, область определения будет всеми значениями x, кроме x = 0, так как деление на ноль не определено.
Какие примеры можно привести области определения функций?
Примеры областей определения функций могут быть разнообразными: для функции f(x) = √x, область определения будет x >= 0, так как извлечение корня из отрицательного числа не определено; для функции g(x) = 1/(x-2), область определения будет x ≠ 2, так как деление на 0 не определено.
Зачем важно знание области определения функции?
Знание области определения функции важно для корректного определения значения функции, избегания ошибок и понимания особенностей поведения функции. Это позволяет избежать ситуаций, когда функция не определена для некоторых значений аргумента и предотвратить некорректные вычисления.



