Умножение скаляра на вектор является одной из основных операций в линейной алгебре и науке о векторах. Эта операция позволяет умножить число (скаляр) на вектор, изменяя его длину и направление. Важно понимать основные принципы и правила умножения скаляра на вектор для решения множества задач в различных областях математики и физики.
Умножение скаляра на вектор происходит путем умножения каждой компоненты вектора на заданное число, что в итоге приводит к изменению длины вектора и/или его направления в пространстве. Эта операция имеет важное значение при работе с линейными преобразованиями и вычислении различных физических величин, связанных с векторами.
Что такое умножение скаляра на вектор
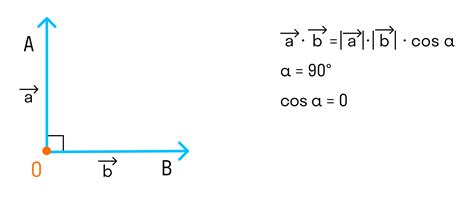
Скаляр и вектор: определения разных типов
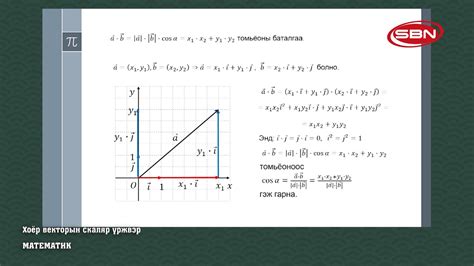
Вектор – величина, которая характеризуется не только численным значением, но и направлением и точкой приложения. Например, сила, скорость, ускорение. Векторы представляются стрелками, длина которых пропорциональна значению величины, а направление указывает направление действия.
Скаляры и векторы играют важную роль в физике, математике и других науках, помогая описывать различные явления и процессы в природе и мире. Понимание различий между ними существенно для корректного математического моделирования и решения задач.
Применение умножения скаляра на вектор

Умножение скаляра на вектор позволяет увеличить или уменьшить вектор по направлению без изменения его направления. Это дает возможность управлять масштабом вектора, что полезно во многих задачах.
Применение умножения скаляра на вектор используется в физике, математике, компьютерной графике, машинном обучении и других областях. Например, масштабирование векторов может быть полезно при изменении размера объектов на экране, а также при решении задач по оптимизации и анализу данных.
Умножение вектора на скаляр происходит путем умножения каждой компоненты вектора на скалярный множитель. Это позволяет изменять длину вектора и сохранять его направление. Если скалярное произведение отрицательное, то вектор будет изменять свое направление.
Применение умножения скаляра на вектор дает возможность эффективно манипулировать векторами и выполнять различные операции с ними в различных областях науки и техники.
Формула умножения скаляра на вектор

Умножение скаляра на вектор представляет собой операцию, при которой каждая компонента вектора умножается на данный скаляр. Это выполняется по формуле:
- Пусть у нас есть вектор 𝑎 = [𝑎₁, 𝑎₂, 𝑎₃] и скаляр 𝑘.
- Тогда результат умножения скаляра на вектор будет:
𝑘𝑎 = [𝑘𝑎₁, 𝑘𝑎₂, 𝑘𝑎₃]
Данная операция позволяет масштабировать вектор, увеличивая или уменьшая его длину и направление в зависимости от значения скаляра.
Геометрическая интерпретация умножения
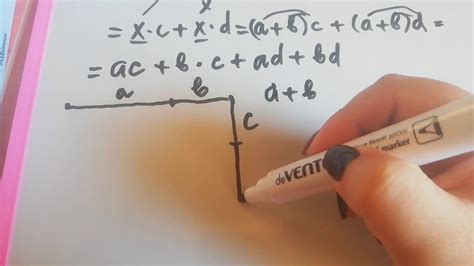
Умножение вектора на скаляр можно геометрически интерпретировать как изменение длины и направления вектора.
При умножении вектора на положительный скаляр, длина вектора увеличивается, а направление остается неизменным.
Если скаляр отрицательный, то длина вектора уменьшается, а направление меняется на противоположное.
Этот принцип применяется в реальном мире при масштабировании графиков, изменении скорости объектов и других физических процессах.
Свойства умножения скаляра на вектор

1. Дистрибутивность относительно сложения векторов: a * (u + v) = a * u + a * v, где a - скаляр, u и v - векторы.
2. Дистрибутивность относительно сложения скаляров: (a + b) * u = a * u + b * u, где a и b - скаляры, u - вектор.
3. Ассоциативность умножения: a * (b * u) = (a * b) * u, где a и b - скаляры, u - вектор.
4. Умножение на нулевой вектор: 0 * u = 0, где u - любой вектор.
Эти свойства помогают в работе с операцией умножения скаляра на вектор, делая ее более понятной и удобной для проведения различных вычислений в линейной алгебре.
Примеры решения задач с умножением

Пример 1: Умножение вектора V = [2, 3] на скаляр k = 3.
Решение: Результат умножения будет [2*3, 3*3] = [6, 9].
Пример 2: Умножение вектора W = [-1, 5, 2] на скаляр а = -2.
Решение: Результат умножения будет [-1*(-2), 5*(-2), 2*(-2)] = [2, -10, -4].
Пример 3: Умножение вектора P = [4, -2, 1] на скаляр b = 0.
Решение: Результат умножения будет [4*0, -2*0, 1*0] = [0, 0, 0].
Вопрос-ответ

Как выполняется умножение скаляра на вектор?
Умножение скаляра на вектор происходит путем умножения каждой компоненты вектора на данный скаляр. Например, если у нас есть вектор (x, y, z) и скаляр k, то произведение будет равно (kx, ky, kz).
В чем заключается геометрическая интерпретация умножения скаляра на вектор?
Геометрически умножение скаляра на вектор приводит к изменению длины вектора и его направления. При умножении на положительный скаляр вектор увеличивается, а при умножении на отрицательный скаляр он меняет направление.
Какие свойства имеет умножение скаляра на вектор?
Умножение скаляра на вектор обладает следующими свойствами: дистрибутивность относительно сложения скаляров, ассоциативность относительно умножения скаляров и скалярного умножения, коммутативность скаляров.
Можно ли умножать вектор на вектор?
В математике вектор на вектор умножать нельзя, однако можно выполнять скалярное и векторное произведение векторов, которые дают в результате скаляр и вектор соответственно.
Какое значение имеет умножение скаляра на вектор в физике?
В физике умножение скаляра на вектор используется для масштабирования векторов, задавая им новые размеры или ориентацию в пространстве. Это помогает в моделировании физических явлений и вычислении различных величин.



