Перевод дроби в десятичное число – важный аспект математики, который часто встречается в повседневной жизни. Перевод дробей в десятичные числа помогает производить точные вычисления и упрощает работу с числами. Дроби выражают отношение части к целому, а десятичные числа представляют собой числа с дробной частью, записанной после десятичной запятой.
Существуют определенные правила, которые необходимо соблюдать при переводе дробей в десятичные числа. Первое правило - необходимо делить числитель дроби на знаменатель. Результат деления будет десятичным числом. Затем дроби можно округлить до нужного количества знаков после запятой или записать в виде периодической десятичной дроби, если она не имеет конечного десятичного представления.
Основные правила

Для того чтобы перевести дробь в десятичное число, необходимо разделить числитель на знаменатель. Результатом этого деления будет периодическое или конечное десятичное число.
Если числитель меньше знаменателя, полученное десятичное число будет меньше единицы. Для корректного представления таких дробей удобно добавить нули перед запятой.
| Пример | Дробь | Десятичное число |
|---|---|---|
| 1 | 2/3 | 0,6666... |
| 2 | 7/4 | 1,75 |
Как переводить дроби
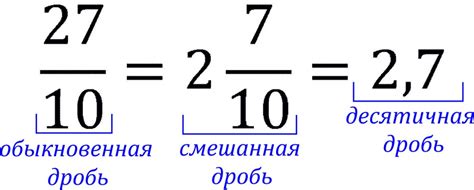
Дроби можно удобно переводить в десятичные числа, если знать базовые правила. Основная идея заключается в том, что дробь представляет собой отношение числителя к знаменателю. Для перевода дроби в десятичное число необходимо разделить числитель на знаменатель. В результате получается десятичная дробь, которую можно округлить до определенного числа знаков после запятой.
| Пример | Перевод в десятичное число |
|---|---|
| 1/2 | 1 ÷ 2 = 0,5 |
| 3/4 | 3 ÷ 4 = 0,75 |
| 5/8 | 5 ÷ 8 = 0,625 |
Важность десятичных чисел

Десятичные числа играют ключевую роль в математике и повседневной жизни. Они позволяют нам легко работать с дробными значениями, измерениями и денежными суммами. Десятичные числа позволяют удобно представлять дробные значения в виде цифр и делать точные вычисления. Они также используются в финансах, науке, технике и многих других областях.
Корректное переведение дробей в десятичные числа позволяет сделать математические операции более простыми и точными, что очень важно в ряде практических ситуаций.
Метод разложения

Для перевода дроби в десятичное число существует метод разложения. Шаги этого метода следующие:
| 1. | Разделить числитель на знаменатель |
| 2. | Полученное значение записать с ограничителем 0 и запятой |
| 3. | Если остаток от деления не равен 0, домножить числитель на 10 и продолжить деление |
Точность вычислений

При переводе дробей в десятичные числа важно сохранять точность вычислений. Для получения точного результата необходимо учитывать все цифры после запятой и не округлять результаты раньше времени.
Например, при делении 1 на 3, результат будет 0.33333..., и продолжение последовательности цифр после запятой может быть бесконечным. При округлении до определенного числа знаков после запятой может потеряться значимая часть числа.
Для сохранения точности вычислений следует работать с дробями в виде десятичных чисел до получения конечного результата.
Примеры расчетов

Пример 1:
- Раздели числитель дроби на знаменатель: 3 ÷ 8 = 0,375.
Пример 2:
- Раздели числитель дроби на знаменатель: 5 ÷ 6 = 0,833.
Пример 3:
- Раздели числитель дроби на знаменатель: 2 ÷ 3 = 0,666.
Применение в жизни
Знание правил перевода дробей в десятичные числа очень полезно в повседневной жизни. Например, при расчетах с валютой, когда нужно перевести дробную долю денежной суммы в десятичное число для точного подсчета. Также данное умение пригодится при расчетах процентов и долей, где необходимо точно определить долю от общей суммы. В сфере научных и технических расчетов также необходимо умение эффективно работать с дробными числами, чтобы получить точные результаты.
| Пример | Применение |
|---|---|
| 1/2 | Перевод доли в десятичное число: 0.5 |
| 3/4 | Использование для расчета процентов: 0.75 |
Вопрос-ответ

Какие правила нужно соблюдать при переводе дробей в десятичные числа?
При переводе дроби в десятичную форму необходимо разделить числитель на знаменатель. Полученное частное будет являться десятичной записью дроби. Например, при переводе дроби 3/4 в десятичное число, мы получим 3 ÷ 4 = 0.75.
Какие дроби можно перевести в десятичные числа без остатка?
Дроби, у которых знаменатель является степенью числа 10 (10, 100, 1000 и т. д.), можно перевести в десятичные числа без остатка. Например, дробь 1/10 будет равна 0.1, дробь 3/100 будет равна 0.03 и т. д.
Каким образом можно упростить перевод периодических дробей в десятичные числа?
Для периодических дробей, где одна или несколько цифр повторяются, можно воспользоваться методом построения уравнения. Например, при переводе дроби 1/3 в десятичное число, мы получаем периодическую дробь 0.(3). Заменим данную дробь на переменную x: x = 0.(3). Умножим x на 10, чтобы перенести период в дробную часть: 10x = 3.(3). Вычитаем из первого уравнения второе: 9x = 3. Отсюда x = 1/3 = 0.(3).



