Графы – это математическая модель, которая используется для представления связей между объектами. Они широко применяются в различных областях, таких как информатика, транспортная логистика, социология и другие. Один из способов представления графа – это матрица инцидентности.
Матрица инцидентности – это двумерный массив, который показывает взаимосвязь между вершинами и рёбрами в графе. Строки матрицы соответствуют вершинам, а столбцы – рёбрам. Если вершина инцидентна ребру, то на пересечении строки вершины с столбцом ребра стоит значение 1, в противном случае 0.
Методы построения графа
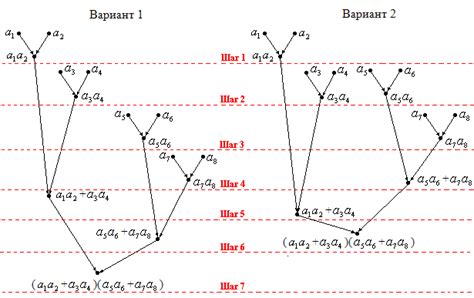
Существует несколько методов построения графа по матрице инцидентности, которые позволяют представить связи между вершинами визуально и наглядно. Некоторые из основных методов включают:
| 1. Метод матрицы смежности: | Для построения графа по матрице инцидентности можно использовать матрицу смежности, где строки и столбцы представляют вершины, а значения в ячейках указывают наличие или отсутствие ребра между вершинами. |
| 2. Применение алгоритмов визуализации: | Существуют различные алгоритмы визуализации графов, такие как алгоритм Фриша-Лейа или алгоритм Холи. Они позволяют эффективно отображать структуру графа на плоскости. |
| 3. Использование специализированных программ: | Для удобного построения и визуализации графов по матрице инцидентности можно воспользоваться специализированными программами, такими как Graphviz, Gephi, yEd и др. |
Алгоритмы определения рёбер
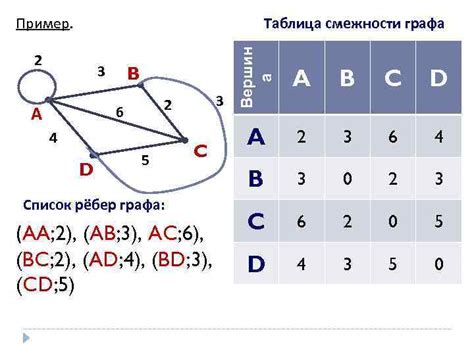
Существует несколько алгоритмов определения рёбер в графе на основе матрицы инцидентности:
- Простой метод: Для каждой пары вершин проверяется, инцидентны ли им одно или несколько рёбер. Если да, то это ребро добавляется в список рёбер.
- Алгоритм проверки инцидентности: Алгоритм обходит матрицу инцидентности и находит рёбра, которые инцидентны указанным вершинам.
Выбор алгоритма зависит от сложности графа и требуемой точности определения рёбер. Каждый из них имеет свои преимущества и недостатки, и может быть применён в различных ситуациях.
Примеры построения графа
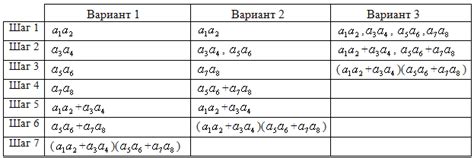
Давайте рассмотрим несколько примеров построения графов на основе матрицы инцидентности:
| Вершины | Рёбра |
|---|---|
| Вершина 1 | Ребро 1, Ребро 2 |
| Вершина 2 | Ребро 1, Ребро 3 |
| Вершина 3 | Ребро 2, Ребро 3 |
Таким образом, мы можем представить граф с тремя вершинами и тремя рёбрами, используя матрицу инцидентности.
Граф с заданной матрицей инцидентности
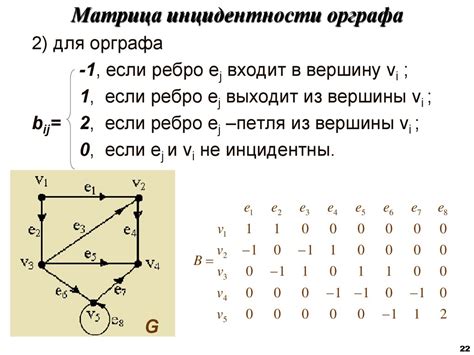
Для построения графа по заданной матрице инцидентности необходимо выполнить следующие шаги:
1. Создание вершин и рёбер
Первым шагом является определение числа вершин и рёбер графа по матрице инцидентности. Каждая строка матрицы инцидентности представляет вершину, а столбцы соответствуют рёбрам. Если элемент матрицы равен 1, то вершина инцидентна ребру, если -1, то вершина инцидентна ребру с противоположной ориентацией.
2. Построение графа
Создаются вершины и рёбра графа в соответствии с матрицей инцидентности. Для каждой строки матрицы создаётся вершина, а для каждого столбца – ребро. Знак элемента определяет ориентацию ребра.
Пример
Пусть дана матрица инцидентности:
| 1 2 3 4 --+--------- 1 | 1 1 0 0 2 |-1 0 1 0 3 | 0 1 1 -1
Для данной матрицы инцидентности нарисуем граф:
(рисунок графа)
Вопрос-ответ

Каким образом можно построить граф по матрице инцидентности?
Для построения графа по матрице инцидентности необходимо следовать нескольким шагам. Во-первых, определить количество вершин и рёбер в графе. Затем составить матрицу инцидентности, где строки соответствуют вершинам, а столбцы – рёбрам. После этого можно нарисовать граф, где вершины соответствуют строкам, а рёбра – столбцам. К примеру, если в матрице инцидентности 1 стоит в ячейке (вершина 1, ребро 1), это значит, что вершина 1 инцидентна ребру 1. Таким образом, построен граф по матрице инцидентности.
Какие методы используются для построения графа по матрице инцидентности?
Существует несколько методов построения графа по матрице инцидентности. Один из наиболее распространенных методов - это метод последовательного добавления вершин и рёбер. Исходя из заданной матрицы инцидентности, поочерёдно добавляются вершины и рёбра, пока не получится граф, соответствующий матрице. Ещё один метод состоит в том, чтобы использовать алгоритмы визуализации графов, которые автоматически строят граф по матрице инцидентности.
Какие практические применения у метода построения графа по матрице инцидентности?
Метод построения графа по матрице инцидентности находит широкое применение в различных областях, таких как теория графов, транспортная логистика, компьютерные сети, биоинформатика и др. Например, в транспортной логистике этот метод используется для моделирования транспортных сетей и оптимизации маршрутов. В биоинформатике метод может применяться для анализа молекулярных взаимосвязей в биологических системах. Таким образом, метод построения графа по матрице инцидентности имеет широкие практические применения.



