Умножение чисел с одинаковыми степенями – одна из базовых операций в алгебре, которая встречается при решении различных задач. Этот процесс может показаться запутанным, но на самом деле все довольно просто, если вы знаете основные правила.
Основной принцип умножения оснований с одинаковыми степенями заключается в том, что для умножения чисел с одинаковыми степенями достаточно перемножить сами числа (основания), и затем возвести в степень их общую степень. Такой подход позволяет с легкостью решать задачи и находить неизвестные значения.
Правила умножения оснований с одинаковыми степенями
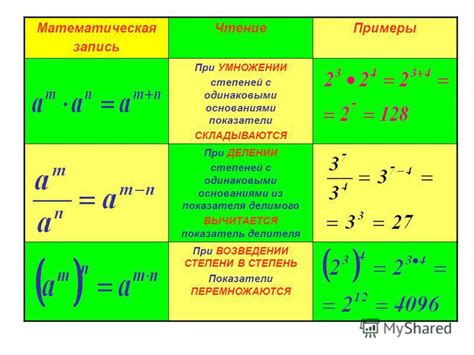
При умножении чисел с одинаковыми степенями, основания перемножаются, а степени складываются. Это правило называется законом степеней.
| Пример | Результат |
|---|---|
| a^m * a^n = a^(m+n) | 2^3 * 2^4 = 2^(3+4) = 2^7 = 128 |
| x^2 * x^3 = x^(2+3) = x^5 | x^2 * x^3 = x^5 |
Основные правила умножения

Для умножения одинаковых оснований с одинаковыми степенями нужно складывать степени и сохранять основание.
Например, a^m * a^m = a^(m+n), где a - основание, m - степень.
Для умножения разных оснований с одинаковыми степенями нужно перемножать основания и сохранять степень.
Например, a^m * b^m = (a*b)^m
Примеры умножения

Рассмотрим несколько примеров умножения оснований с одинаковыми степенями:
| Пример | Выражение | Результат |
| Пример 1 | 23 * 23 | 26 = 64 |
| Пример 2 | 52 * 52 | 54 = 625 |
| Пример 3 | 104 * 104 | 108 = 100000000 |
Практические задачи на умножение

Решим несколько практических задач на умножение оснований с одинаковыми степенями:
| Задача | Решение |
|---|---|
| 1. Вычислите \(2^3 \cdot 2^3\) | \(2^3 \cdot 2^3 = 2^{3+3} = 2^6 = 64\) |
| 2. Упростите \(5^4 \cdot 5^2\) | \(5^4 \cdot 5^2 = 5^{4+2} = 5^6 = 15625\) |
| 3. Посчитайте \(3^5 \cdot 3^5\) | \(3^5 \cdot 3^5 = 3^{5+5} = 3^{10} = 59049\) |
Тренировка по умножению

Давайте потренируемся в умножении оснований с одинаковыми степенями! Возьмем, например, выражение a^m * a^m. Для умножения таких выражений нужно сложить степени основания a, то есть получится a^(m + m) = a^(2m). Пример: 2^3 * 2^3 = 2^(3 + 3) = 2^6.
Теперь попробуйте решить следующее упражнение: 3^4 * 3^4.
1. Сначала сложите степени основания 3: 4 + 4 = 8.
2. Получится: 3^4 * 3^4 = 3^8.
Ответ: 3^8.
Практикуйтесь в умножении оснований с одинаковыми степенями для лучшего понимания и запоминания правил!
Вопрос-ответ

Как правильно умножать основания с одинаковыми степенями?
Для умножения оснований с одинаковыми степенями нужно сохранить основание и сложить степени. Например, a^3 * a^5 = a^(3+5) = a^8.
Почему при умножении оснований с одинаковыми степенями их степени складываются?
При умножении оснований с одинаковыми степенями степени складываются, потому что это соответствует тому, как проводится операция умножения в алгебре. Мы работаем с одним и тем же основанием, поэтому просто суммируем их степени.
Можете привести практический пример умножения оснований с одинаковыми степенями?
Конечно! Например, умножим a^2 * a^4. По правилу умножения оснований с одинаковыми степенями мы должны сложить степени, получим a^(2+4) = a^6. Таким образом, a^2 * a^4 = a^6.



