Геометрическая прогрессия – это последовательность чисел, в которой каждый следующий элемент получается умножением предыдущего на некоторое число, называемое знаменателем. Если знаменатель равен 2, то получается геометрическая прогрессия степеней числа 2.
Для проверки геометрической прогрессии степеней числа 2 необходимо последовательно вычислять каждый элемент последовательности. Если каждый последующий элемент равен предыдущему, умноженному на 2, то можно утверждать, что последовательность является геометрической прогрессией.
Пример: 2, 4, 8, 16, 32. В данной последовательности каждый элемент равен предыдущему, умноженному на 2, что подтверждает геометрическую прогрессию степеней числа 2.
Проверка геометрической прогрессии

Пусть у нас есть последовательность \(2, 4, 8, 16, 32, 64, ...\). Для проверки, является ли эта последовательность геометрической прогрессией, можно взять любые последовательные члены и найти их отношение.
Например, для чисел 8 и 16: \(16 / 8 = 2\). Проводим такую же операцию для других пар чисел. Если отношение всех пар чисел одинаково, то данная последовательность является геометрической прогрессией.
Изучение степеней числа 2
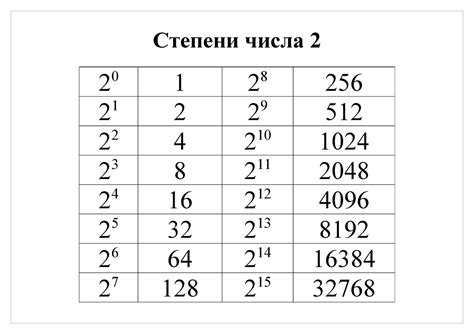
Изучая степени числа 2, можно заметить закономерности и использовать их в математических расчетах, программировании и других областях.
- 2^0=1
- 2^1=2
- 2^2=4
- 2^3=8
Методы определения прогрессии

1. Проверка отношения элементов: Для геометрической прогрессии отношение любых двух последовательных элементов должно быть одинаковым. То есть, если a, b и c - три последовательных члена прогрессии, то должно выполняться условие b / a = c / b.
2. Проверка разности логарифмов: Для арифметической прогрессии логарифмы элементов последовательности различаются на постоянное число, в случае геометрической прогрессии логарифмы элементов должны различаться на постоянное число.
3. Другие способы: Дополнительно можно использовать формулы для суммы элементов геометрической прогрессии, а также сравнение элементов с общим знаменателем геометрической прогрессии.
Анализ геометрической последовательности

Геометрическая прогрессия представляет собой последовательность чисел, каждое следующее из которых получается умножением предыдущего числа на одно и то же число, называемое знаменателем прогрессии.
Для анализа геометрической последовательности необходимо определить знаменатель прогрессии и рассчитать следующие члены последовательности по формуле a(n) = a(1) * r^(n-1), где a(n) - n-й член последовательности, a(1) - первый член последовательности, r - знаменатель прогрессии, n - номер члена последовательности.
Пример геометрической последовательности: 2, 4, 8, 16, 32. Здесь знаменатель прогрессии равен 2. Для расчета следующих членов последовательности необходимо умножить предыдущий член на 2: 32 * 2 = 64, 64 * 2 = 128 и так далее.
Примеры расчета прогрессии

Пример 1:
- Начальное число: 2
- Шаг прогрессии: 2
- Первые 5 членов прогрессии:
- 2
- 4
- 8
- 16
- 32
Пример 2:
- Начальное число: 1
- Шаг прогрессии: 3
- Первые 4 члена прогрессии:
- 1
- 3
- 9
- 27
Расчет первого члена и знаменателя геометрической прогрессии

Для расчета знаменателя прогрессии (q) необходимо взять любой член прогрессии и поделить его на предыдущий член. Формула вычисления знаменателя: q = аₙ / аₙ₋₁, где аₙ - любой член прогрессии, аₙ₋₁ - предыдущий член.
Проверка геометрической прогрессии

Пример: последовательность 2, 4, 8, 16. Проверяем отношения: 4/2 = 2, 8/4 = 2, 16/8 = 2. Отношения равны 2, значит, данная последовательность является геометрической прогрессией.
Использование математических формул

Сравнение с другими типами прогрессий

Геометрическая прогрессия степеней числа 2 имеет свои особенности, которые отличают ее от других типов прогрессий. Сравним ее с арифметической и квадратичной прогрессиями.
1. Арифметическая прогрессия: В арифметической прогрессии каждый следующий элемент отличается от предыдущего на постоянную величину, называемую разностью. В то время как в геометрической прогрессии каждый элемент получается умножением предыдущего на постоянное число.
2. Квадратичная прогрессия: В квадратичной прогрессии каждый элемент получается путем добавления фиксированной константы к квадрату натурального числа. Эта прогрессия отличается от геометрической тем, что элементы увеличиваются не путем умножения, а путем сложения.
Таким образом, геометрическая прогрессия степеней числа 2 представляет собой уникальный тип прогрессии, отличающийся от других по способу получения следующих элементов.
Практическое применение в задачах

Геометрическая прогрессия степеней числа 2 широко применяется в информационных технологиях, математике, физике и других областях. Например, если нам нужно вычислить скорость роста некоторого процесса, который удваивается каждую минуту, то мы можем использовать понятие геометрической прогрессии, где каждый следующий элемент вдвое больше предыдущего.
Еще одним практическим примером является расчет объема памяти компьютера, который увеличивается в соответствии с геометрической прогрессией. Если начальный объем памяти 2 Гб, а каждую неделю он увеличивается вдвое, то мы можем использовать формулу геометрической прогрессии для прогнозирования объема памяти через определенный период времени.
Таким образом, понимание и применение геометрической прогрессии степеней числа 2 помогает в решении различных задач, связанных с экспоненциальным ростом или убыванием в различных областях науки и техники.
Вопрос-ответ

Зачем нужно проверять геометрическую прогрессию степеней числа 2?
Проверка геометрической прогрессии степеней числа 2 позволяет определить, соответствует ли последовательность степеней числа 2 определенному правилу и выявить закономерности в росте степеней. Это полезно для анализа данных, построения прогнозов и решения различных задач, связанных с экспоненциальным ростом.
Какие методы можно использовать для проверки геометрической прогрессии степеней числа 2?
Для проверки геометрической прогрессии степеней числа 2 можно использовать методы анализа отношения соседних членов последовательности, вычисления отношения любых двух соседних членов, а также проверку соответствия формуле для геометрической прогрессии an = a1 * r^(n-1), где a1 = 2^0, r = 2. При этом необходимо учитывать особенности вычислений и обратить внимание на пределы точности.



