Прямая и обратная задача – это термины, широко используемые в математике и других науках, чтобы обозначить два разных подхода к решению задач. Прямая задача предполагает нахождение решения исходной проблемы на основе предоставленных данных, в то время как обратная задача заключается в определении входных параметров, обеспечивающих определенный результат.
Основное отличие между прямой и обратной задачей заключается в направлении процесса решения проблемы. В прямой задаче вы начинаете с известных данных и ищете решение, а в обратной задаче вам нужно определить параметры, которые приведут к конкретному результату. Оба подхода имеют свои уникальные особенности и широко применяются в различных областях науки и техники.
Прямая задача: суть и назначение
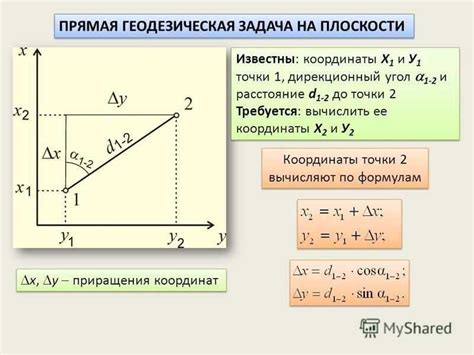
Прямая задача в контексте математики и науки о данных относится к процессу нахождения решения искомого значения на основе входных данных и известных параметров. Основное назначение прямой задачи заключается в предсказании результатов на основе имеющейся информации и параметров модели. Этот процесс применяется в различных областях, таких как машинное обучение, статистика и физика, для прогнозирования и анализа данных.
Прямая задача часто используется как основа для обратной задачи, которая, напротив, заключается в определении параметров модели на основе наблюдаемых данных. Важно отметить, что прямая задача играет ключевую роль в научных и инженерных исследованиях, помогая определять результаты и эффективность моделей.
Объяснение прямой задачи в математике

Обратная задача: определение и примеры
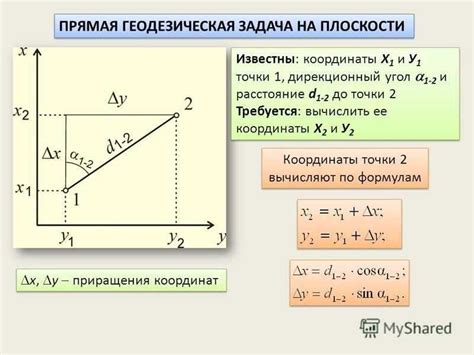
Пример обратной задачи в математике - задача определения функции, удовлетворяющей некоторому условию. Например, если известны значения функции на некотором промежутке, найти саму функцию, удовлетворяющую этим значениям.
В физике обратные задачи часто возникают при восстановлении свойств среды по измеренным данным. Например, в медицине обратные задачи могут быть связаны с восстановлением формы и структуры внутренних органов по данным медицинских изображений.
Различие между прямой и обратной задачей

- Прямая задача: В прямой задаче известны входные данные и модель, требуется найти выходные данные. Например, если известны параметры объекта и его окружения, можно предсказать его поведение или характеристики.
- Обратная задача: В обратной задаче имеются выходные данные и модель, нужно найти входные данные. Это более сложная задача, так как требуется распознать скрытые параметры системы по наблюдаемым результатам.
Таким образом, основное различие между прямой и обратной задачей заключается в том, что в первом случае ищется результат на основе входных данных, а во втором - входные данные определяются по результатам.
Основные отличия между прямой и обратной задачей
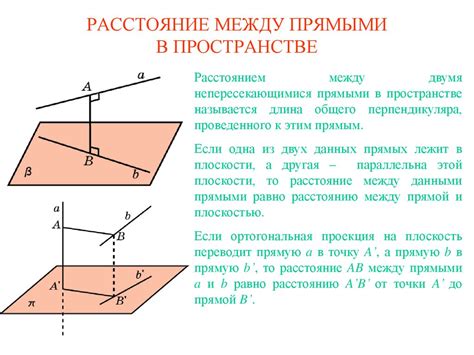
- Прямая задача: В прямой задаче требуется определить выходные параметры системы или процесса на основе заданных входных данных и известных законов или алгоритмов. То есть, имея начальные условия, мы стремимся к выходным результатам.
- Обратная задача: В обратной задаче наоборот, необходимо определить входные параметры или условия, исходя из известных выходных данных. То есть, по заданным выходным результатам мы ищем начальные условия или параметры.
Таким образом, прямая задача описывает процесс прогнозирования результатов системы, в то время как обратная задача представляет собой процесс инверсии данных для нахождения начальных условий или параметров.
Вопрос-ответ

Чем отличается прямая задача от обратной?
Прямая задача и обратная задача - два основных типа задач, которые решаются в различных областях науки и техники. Прямая задача заключается в поиске решения, исходя из известных параметров и условий. В то время как обратная задача предполагает нахождение неизвестных параметров и условий, исходя из результата. Таким образом, основное отличие между прямой и обратной задачами заключается в постановке задачи и направлении решения.
Можете привести примеры прямой и обратной задачи?
Пример прямой задачи: если у нас есть уравнение движения тела, мы можем найти его траекторию, зная начальные параметры такие как скорость и ускорение. Пример обратной задачи: если мы знаем траекторию движения тела, мы можем обратно вычислить начальные параметры, такие как скорость и ускорение, используя обратные методы.



