Квадрат - одна из известных геометрических фигур, у которой все стороны равны друг другу и все углы прямые. Диагональ квадрата - это отрезок, соединяющий противоположные углы. Интересно, что прямая, проходящая через середину диагонали квадрата, имеет ряд удивительных свойств, которые можно изучить при помощи геометрического анализа.
Для начала, стоит обратить внимание на то, что середина диагонали квадрата является центром его описанной окружности. Это означает, что прямая, проходящая через середину диагонали, будет являться диаметром этой окружности. Таким образом, она будет перпендикулярна к диагонали квадрата и разделит ее на две равные части.
Также стоит отметить, что прямая, проходящая через середину диагонали квадрата, делит его на два равных прямоугольных треугольника. Это отличное поле для применения теорем Пифагора и косинусов, что позволяет дополнительно исследовать свойства данной прямой и ее взаимное расположение относительно сторон квадрата.
Геометрия и ее основные принципы

Главными объектами изучения в геометрии являются точки, прямые, плоскости, углы, отрезки, окружности и другие фигуры. Важным принципом геометрии является метод доказательств – логическая цепочка утверждений, подтверждающих истинность какого-либо утверждения или теоремы.
Геометрический анализ прямой через середину диагонали квадрата является примером применения геометрических принципов для нахождения свойств и характеристик геометрических фигур.
Середина диагонали квадрата и ее свойства
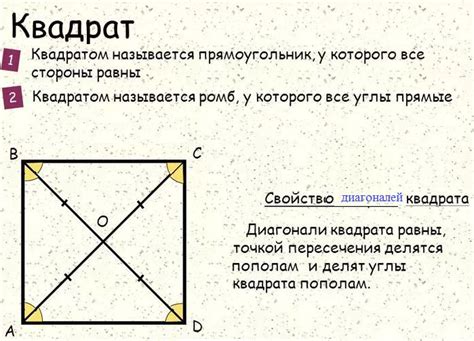
Свойства середины диагонали квадрата:
- Центр вписанного круга, описывающего квадрат.
- Точка симметрии относительно центра квадрата.
- Расстояние от середины диагонали до любой вершины квадрата равно половине длины диагонали.
Прямая: определение и основные характеристики
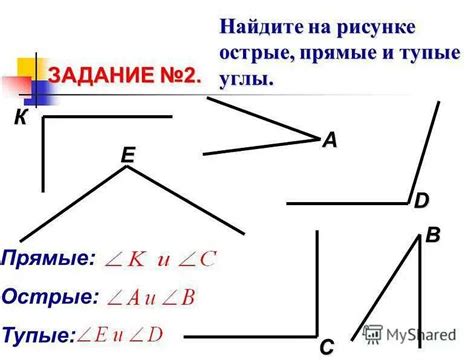
Основные характеристики прямой:
1. Прямая не имеет начала или конца, она бесконечна в обе стороны.
2. Прямая определяется двумя точками, через которые можно провести прямую. Данная прямая будет проходить через эти точки и не иметь изгибов.
3. На прямой можно провести любое число точек, и они все будут лежать на этой прямой.
Анализ геометрической задачи через середину диагонали
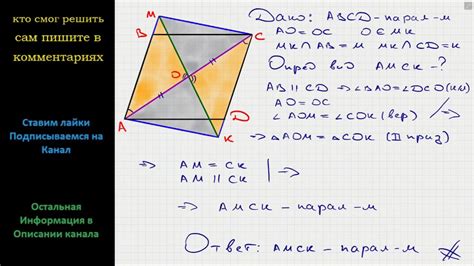
Рассмотрим геометрическую задачу, связанную с квадратом. Допустим, у нас есть квадрат, и мы хотим найти прямую, проходящую через его середину диагонали. Эта задача требует рассмотрения свойств квадрата и использования геометрических методов для ее решения.
Первым шагом является построение квадрата и его диагоналей. Середина диагонали квадрата является точкой пересечения диагоналей и одновременно является центром квадрата. Из этого следует, что прямая, проходящая через середину диагонали, будет проходить через центр квадрата.
Таким образом, мы можем найти уравнение прямой, проходящей через середину диагонали квадрата, зная координаты центра квадрата и используя уравнение прямой в общем виде. Это позволяет нам более точно анализировать геометрическое положение прямой относительно квадрата и его диагоналей.
Способы определения углового коэффициента прямой

| Метод | Формула |
|---|---|
| 1. Из уравнения прямой | Если уравнение прямой имеет вид y = kx + b, то угловой коэффициент равен k. |
| 2. Из двух точек на прямой | Пусть на прямой есть две точки A(x₁, y₁) и B(x₂, y₂). Тогда угловой коэффициент равен (y₂ - y₁) / (x₂ - x₁). |
| 3. Графический метод | На координатной плоскости проводится прямая, и определяется её угловой наклон относительно оси абсцисс. |
Влияние середины диагонали на уравнение прямой

Пусть прямая имеет уравнение y = kx + b. Так как прямая проходит через середину диагонали, координаты этой точки будут (0, 0), поскольку середина диагонали всегда проходит через начало координат. Следовательно, зная координаты середины диагонали, мы можем определить уравнение прямой, проходящей через нее.
Практическое применение геометрического анализа прямой
Геометрический анализ прямой часто применяется при проектировании зданий и строительстве, например, при построении фундамента или разметке строительного участка. Точное определение направления прямой и ее расположение в пространстве помогает инженерам и архитекторам создавать устойчивые и эстетичные конструкции.
Также геометрический анализ прямой используется в навигации и картографии. При создании карт и планов необходимо корректно отображать направление движения прямой (например, дороги или реки) для удобства пользователя. Анализ прямой позволяет правильно располагать объекты на карте и обеспечивать точную навигацию.
Вопрос-ответ

Какие методы используются в геометрическом анализе прямой через середину диагонали квадрата?
В геометрическом анализе прямой через середину диагонали квадрата используются методы, основанные на свойствах квадрата и его диагоналей. Например, для определения углового коэффициента прямой можно воспользоваться формулой tg α = 2. Для нахождения уравнения прямой через середину диагонали квадрата можно использовать его координаты и свойства перпендикулярности отрезков.
Как выглядит уравнение прямой через середину диагонали квадрата?
Уравнение прямой через середину диагонали квадрата имеет вид y = kx + c, где k - угловой коэффициент прямой, а c - свободный член. Для квадрата это уравнение может быть найдено с использованием координат середины диагонали и свойств перпендикулярности сторон квадрата.
Какие свойства квадрата помогают анализировать прямую через середину диагонали?
Для анализа прямой через середину диагонали квадрата можно использовать следующие свойства квадрата: одна из диагоналей делит его на два равных треугольника, противоположные стороны квадрата параллельны, и диагонали перпендикулярны друг другу. Эти свойства помогают определить уравнение прямой и ее коэффициенты.
Какие вычисления необходимо провести для анализа прямой через середину диагонали квадрата?
Для анализа прямой через середину диагонали квадрата необходимо вычислить координаты середины диагонали квадрата, определить угловой коэффициент прямой, а затем записать уравнение прямой в виде y = kx + c. Это позволит провести геометрический анализ прямой на плоскости, проходящей через середину диагонали квадрата.



