Дискриминант - это математическое понятие, которое является ключевым при анализе уравнений квадратичной функции. Он позволяет определить, сколько корней имеет уравнение и как они расположены на координатной плоскости. Дискриминант играет важную роль при построении графика функции и понимании её поведения.
Что такое дискриминант

| Значение дискриминанта D | Тип корней |
|---|---|
| D > 0 | Два различных вещественных корня |
| D = 0 | Один вещественный корень (корень кратности 2) |
| D < 0 | Два комплексных корня |
Понятие и значение

Использование дискриминанта при построении графика функции помогает определить вершины параболы, точки пересечения с осями координат, а также общее поведение функции. Знание значения дискриминанта позволяет детально и точно изучать характеристики квадратных уравнений и предсказывать их графическое представление.
Методика вычисления дискриминанта

Для квадратного уравнения вида \(ax^2 + bx + c = 0\) дискриминант \(D\) вычисляется по формуле:
| Для уравнения \(ax^2 + bx + c = 0\) | Дискриминант \(D = b^2 - 4ac\) |
После вычисления дискриминанта можно определить, какие типы корней имеет уравнение:
- Если \(D > 0\), то у уравнения два различных действительных корня.
- Если \(D = 0\), то у уравнения два одинаковых действительных корня.
- Если \(D < 0\), то у уравнения два комплексных корня.
Формула и примеры расчета

Дискриминант квадратного уравнения можно вычислить по формуле:
Д = b^2 - 4ac
Где a, b, c - коэффициенты квадратного уравнения ax^2 + bx + c = 0.
Пример 1:
Рассмотрим уравнение x^2 - 2x - 3 = 0.
Здесь a = 1, b = -2, c = -3.
Вычислим дискриминант:
D = (-2)^2 - 4*1*(-3) = 4 + 12 = 16
Таким образом, D = 16.
Пример 2:
Рассмотрим уравнение 3x^2 + 6x + 3 = 0.
Здесь a = 3, b = 6, c = 3.
Вычислим дискриминант:
D = 6^2 - 4*3*3 = 36 - 36 = 0
Таким образом, D = 0.
Значение дискриминанта для графика
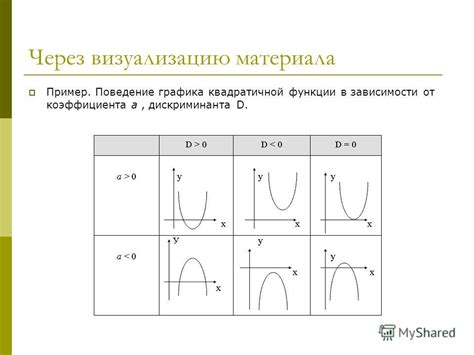
Если дискриминант больше нуля, то график функции будет пересекать ось абсцисс в двух точках, что соответствует наличию двух корней у квадратного уравнения. Это часто означает, что функция имеет вогнутую или выпуклую форму.
Если дискриминант равен нулю, то график функции будет касаться оси абсцисс в одной точке, что соответствует наличию одного корня у квадратного уравнения. Это обычно соответствует параболе, которая касается оси абсцисс.
Если дискриминант меньше нуля, то у квадратного уравнения нет корней, что означает, что график функции не пересекает ось абсцисс. В этом случае парабола либо полностью находится выше оси абсцисс, либо полностью ниже.
Влияние на форму функции
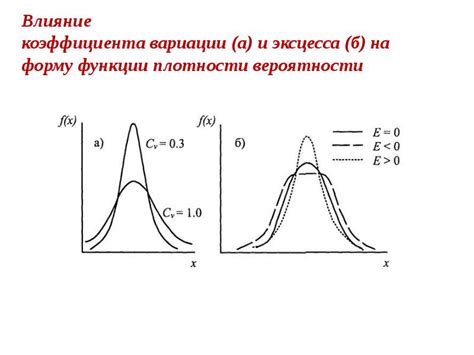
Знание дискриминанта функции позволяет определить ее форму и особенности. В зависимости от значения дискриминанта, функция может иметь различное количество корней и тип графика.
| Значение дискриминанта | Тип графика |
|---|---|
| D > 0 | График функции пересекает ось абсцисс в двух точках |
| D = 0 | График функции касается оси абсцисс в одной точке |
| D < 0 | График функции не пересекает ось абсцисс |
Применение дискриминанта в аналитике

В аналитике дискриминант играет ключевую роль при анализе функций и построении графиков. Значение дискриминанта определяет тип корней уравнения: если дискриминант равен нулю, то уравнение имеет один корень; если дискриминант больше нуля, то уравнение имеет два различных корня; если дискриминант меньше нуля, то уравнение не имеет вещественных корней.
При анализе функций при помощи дискриминанта можно определить существование и количество экстремумов, провести исследование на монотонность функции и определить промежутки возрастания и убывания функции.
Таким образом, понимание и использование дискриминанта в аналитике значительно упрощает анализ функций и помогает строить точные графики.
Вопрос-ответ

Что такое дискриминант и для чего он используется при построении графика функции?
Дискриминант - это параметр квадратного уравнения, который позволяет определить количество и характер корней этого уравнения. При построении графика функции дискриминант помогает определить тип пересечения графика с осью абсцисс и другие ключевые точки.
Как можно вычислить дискриминант квадратного уравнения?
Дискриминант квадратного уравнения вычисляется по формуле: D = b^2 - 4ac, где a, b, c - коэффициенты квадратного уравнения ax^2 + bx + c = 0. Зная значение дискриминанта, можно определить характер корней уравнения.
Чему равно значение дискриминанта, если уравнение имеет два вещественных корня?
Если у квадратного уравнения есть два вещественных корня, то значение дискриминанта D будет больше 0: D > 0. Это свидетельствует о том, что график функции пересекает ось абсцисс дважды.
Какие выводы можно сделать, если дискриминант равен нулю?
Если значение дискриминанта квадратного уравнения равно нулю (D = 0), то это означает, что у уравнения есть один вещественный корень. График функции касается оси абсцисс в одной точке.
Что означает ситуация, когда дискриминант меньше нуля?
Если значение дискриминанта квадратного уравнения отрицательно (D < 0), то у уравнения нет вещественных корней. На графике функции это будет проявляться в том, что график не пересекает ось абсцисс вообще.



