Сложение корней - одна из основных операций алгебры, которая играет важную роль в многих математических задачах. При сложении корней, необходимо правильно вычислить сумму значений подкорневых выражений и привести результат к простейшему виду.
Существуют различные методы вычисления суммы корней, которые позволяют эффективно решать задачи с использованием алгебраических выражений. Один из основных методов - сведение подкорневых выражений к общему знаменателю и последующее сложение.
Для успешного сложения корней необходимо учитывать условия, при которых операция допустима. Например, корни должны иметь одинаковое основание, а иногда требуется рационализация выражений для удобства вычислений.
Вычисление корней уравнений

Для нахождения корней уравнений существует несколько различных методов, в зависимости от типа уравнения и доступных данных. Наиболее распространенные методы включают метод Ньютона, метод половинного деления (бисекции) и метод итерационной дихотомии.
Метод Ньютона, также известный как метод касательных, применяется для нахождения корня уравнения с использованием производной функции. Он обеспечивает быструю сходимость к корню, если начальное приближение достаточно близко к корню.
Метод половинного деления использует свойство непрерывности функции для нахождения корня путем проверки знака функции в различных точках интервала. Этот метод надежен, но может потребовать большего числа итераций для достижения точности.
Метод итерационной дихотомии представляет собой комбинацию методов Ньютона и половинного деления, что позволяет быстрее приблизиться к корню уравнения.
Метод нахождения корней
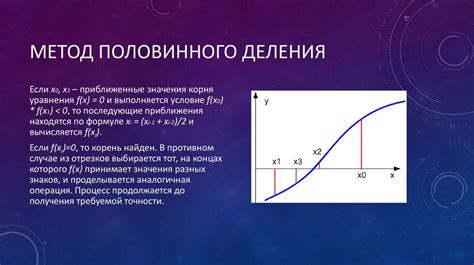
Методы нахождения корней широко применяются в математике, физике, инженерии и других областях для решения уравнений и определения значений переменных. При выборе метода нахождения корней необходимо учитывать точность вычислений, скорость сходимости и возможность нахождения всех корней уравнения.
Алгоритм сложения корней

Простейшим способом сложения корней является использование общего множителя в качестве знаменателя. Например, если у нас есть корни sqrt(a) и sqrt(b), то можно сложить их, если a и b соответственно являются квадратами целых чисел, например a = x^2 и b = y^2, где x и y - целые числа.
После приведения корней к общему знаменателю, мы можем сложить числители и получить результат сложения корней.
Вопрос-ответ

Какие методы можно использовать для сложения корней?
Для сложения корней можно использовать метод приведения подобных и метод подстановки. Метод приведения подобных применяется, когда выражения имеют одинаковые значения под корнем. Метод подстановки используется, когда корни не приводятся под одну знаменательную степень.
Какие условия необходимо учитывать при сложении корней?
При сложении корней необходимо учитывать, что только корни одинаковой степени могут быть сложены вместе. Также важно учитывать знаки перед корнями и следить за тем, чтобы основания корней были равными или приводимыми к одному значению.
Какой результат может быть при сложении корней?
Результатом сложения корней может быть новое выражение под корнем, которое представляет собой корень суммы или разности оснований исходных корней, если условия выполняются.
Как происходит вычисление сложения корней?
Для вычисления сложения корней необходимо привести корни к одной степени и затем сложить или вычесть основания корней в зависимости от знаков. После этого можно провести операции над найденными значениями под корнями.



