В геометрии одной из основных задач является доказательство соответствующих утверждений о геометрических фигурах. Одним из таких утверждений является равенство или параллельность прямых и плоскостей. Для этого существуют различные методы доказательства, которые помогают убедиться в их правильности.
Другим методом доказательства является метод дополнительных углов. По этому методу можно доказать параллельность линий или равенство углов, используя свойства дополнительных углов. Если заданные углы образуют дополнительные углы по отношению к некоторым прямым или плоскостям, то это дает основание для утверждения о равенстве или параллельности.
Изучение свойств прямых
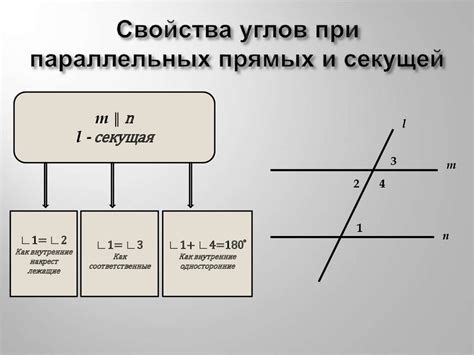
- Прямая определяется двумя различными точками. Для задания прямой необходимо указать две точки, через которые она проходит.
- Прямая делит плоскость на две полуплоскости. Плоскость, через которую проходит прямая, разбивается на две части: область слева от прямой и область справа от нее.
- Прямая может быть перпендикулярна или параллельна другой прямой. Две прямые перпендикулярны, если угол между ними равен 90 градусам. Две прямые параллельны, если они не пересекаются и лежат в одной плоскости.
- Прямая может быть отражена, повернута или сдвинута. Преобразования прямых позволяют изменять их положение и ориентацию на плоскости.
Метод анализа геометрических фигур
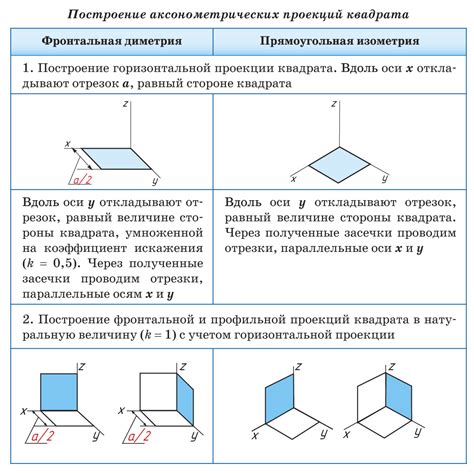
Применение геометрических аксиом
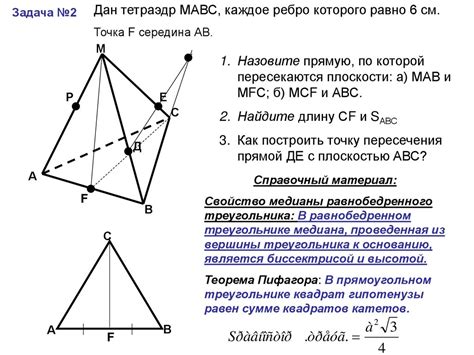
| № | Геометрическая аксиома | Применение |
|---|---|---|
| 1 | Аксиома о непрерывности | Позволяет утверждать, что прямая имеет бесконечное количество точек и непрерывна. |
| 2 | Аксиома о сравнении отрезков | Необходима для сравнения длин отрезков, что важно при доказательстве параллельности. |
| 3 | Аксиома о равенстве углов | Используется для доказательства равенства углов при пересечении прямых. |
Описание основных свойств углов
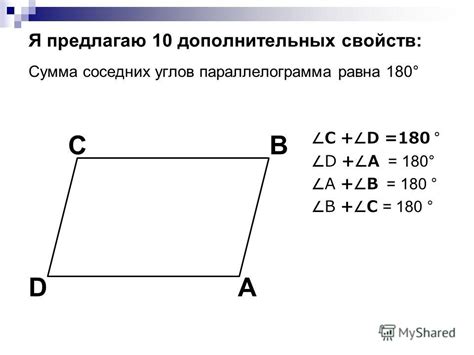
Смежные углы - это углы, у которых общая сторона и вершина, причем сумма их мер равна 180 градусов.
Парные углы - это углы на противоположных сторонах пересекающейся прямой, сумма измерений которых равна 180 градусов.
Использование теоремы о параллельных прямых
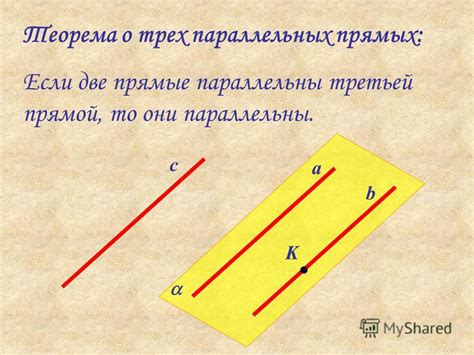
Для доказательства параллельности двух прямых при помощи теоремы о параллельных прямых необходимо применить следующий подход:
Шаг 1: Пусть даны две прямые a и b, исходно нам неизвестно, параллельны они или нет.
Шаг 2: Предположим, что a и b не параллельны, тогда эти прямые пересекаются.
Шаг 3: Рассмотрим другие прямые, параллельные прямой a, проведем перпендикуляр к прямой a из точки пересечения с прямой b.
Шаг 4: Подтверждение того, что данные прямые параллельны, будет нахождение углов, равных друг другу, что доказывает, что прямые a и b также параллельны.
Таким образом, использование теоремы о параллельных прямых позволяет нам доказать параллельность прямых с помощью перпендикуляров и равенства углов.
Применение метода доказательства угла
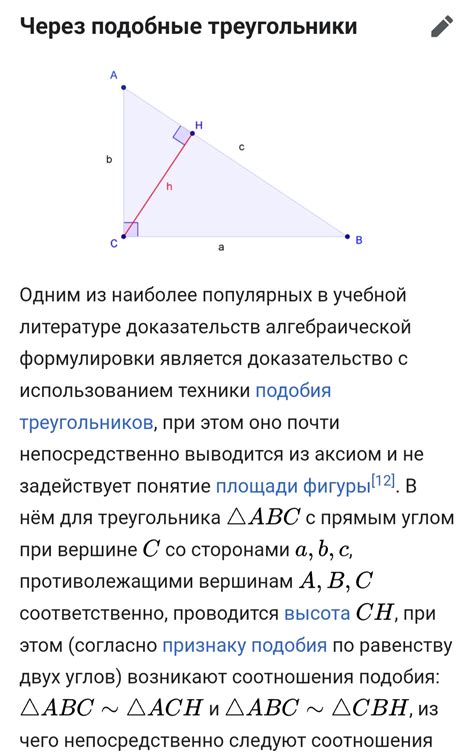
Метод доказательства угла применяется при решении задач на построение прямой, проходящей через заданный угол. Для этого используется таблица с углами и их значениями, а также соответствующие вычисления.
| Угол | Значение угла |
|---|---|
| Прямой угол | 90 градусов |
| Острый угол | менее 90 градусов |
| Тупой угол | более 90 градусов |
При помощи метода доказательства угла можно определить, какая прямая проходит через данный угол или параллельна ему, что позволяет эффективно решать геометрические задачи.
Вопрос-ответ

Как доказать, что две прямые параллельны третьей?
Для доказательства параллельности двух прямых третьей применяется метод параллельных линий. Если две прямые параллельны одной и той же третьей, то углы между ними равны. Этот метод позволяет установить параллельность прямых.
Какие методы используются для доказательства прямых и параллельных третьей?
Основные методы доказательства прямых и параллельных третьей - это метод понижающих перпендикуляров, метод прямых углов, метод определения углов и метод параллельных линий. Каждый из этих методов имеет свои особенности и принципы.
Почему метод прямых углов является одним из основных для доказательства прямых и параллельных третьей?
Метод прямых углов используется для доказательства прямых и параллельных третьей, потому что угол, равный 90 градусов, делит прямую на две равные части. Этот метод позволяет установить равенство углов и доказать параллельность прямых линий.
Каким образом метод понижающих перпендикуляров применяется для доказательства прямых и параллельных третьей?
Метод понижающих перпендикуляров используется для доказательства прямых и параллельных третьей путем установления равенства углов или отрезков, образованных перпендикуляром. Этот метод позволяет делать выводы о параллельности и равенстве сторон прямоугольников и треугольников.
Какие методы можно применить для доказательства прямых и параллельных третьей в геометрии?
Для доказательства прямых и параллельных третьей в геометрии можно применить методы понижающих перпендикуляров, прямых углов, определения углов и параллельных линий. Каждый из этих методов играет важную роль при построении доказательств в геометрии.



