Окружность - это геометрическое тело, представляющее собой множество точек, равноудаленных от центра. Она является одной из основных фигур в геометрии и имеет множество свойств и характеристик.
Диаметр окружности – это отрезок, соединяющий две противоположные точки её наибольшей длины. Диаметр проходит через центр окружности и является одним из ключевых элементов, определяющих её размер и форму.
Взаимосвязь между окружностью и диаметром заключается в том, что диаметр является максимальным отрезком, который можно провести внутри окружности. Диаметр делит окружность на две равные части, называемые полуокружностями, и играет важную роль при вычислении других характеристик окружности, таких как радиус, длина окружности и площадь круга.
Окружность: определение, формула и свойства
Формула окружности выражается следующим образом:
Уравнение окружности: (x - a)^2 + (y - b)^2 = r^2, где (a, b) – координаты центра окружности, r – радиус окружности.
Свойства окружности:
- Радиус окружности представляет собой отрезок, соединяющий центр окружности с любой точкой окружности.
- Диаметр окружности равен удвоенному радиусу и проходит через центр окружности.
- Через любые три точки, не лежащие на одной прямой, можно провести окружность.
Радиус и диаметр окружности: каковы различия
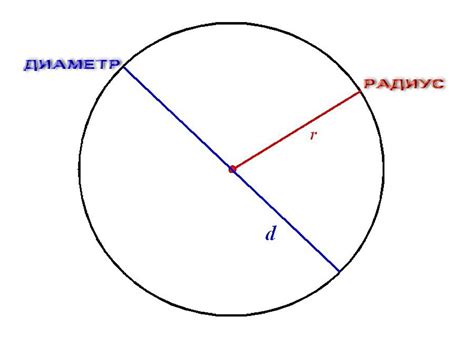
Радиус окружности (R) - это отрезок, соединяющий центр окружности с любой точкой на окружности. Диаметр окружности (D) - это отрезок, соединяющий две противоположные точки на окружности через ее центр.
Основное различие между радиусом и диаметром заключается в их длине. Диаметр в два раза больше радиуса (D = 2R). Таким образом, радиус и диаметр взаимосвязаны соотношением: диаметр равен удвоенному радиусу.
Зная одну из этих характеристик, можно легко вычислить другую. Например, если известен радиус окружности, то диаметр можно найти, умножив радиус на 2. И наоборот, если известен диаметр, радиус можно найти, разделив диаметр на 2.
Окружность и ее диаметр: важное понятие в геометрии
Взаимосвязь окружности и ее диаметра в математике
Диаметр окружности – это отрезок, соединяющий две противоположные точки на окружности, проходящий через центр.
Замечательное свойство окружности: диаметр является наибольшей из всех возможных хорд данной окружности.
Диаметр можно использовать для различных вычислений окружности: длина диаметра вдвое больше радиуса, а площадь круга в четыре раза больше квадрата радиуса.
Таким образом, диаметр и окружность тесно связаны между собой и играют важную роль в математике и геометрии.
Вопрос-ответ

Чем отличается окружность от диаметра?
Окружность - это геометрическое множество точек на плоскости, равноудаленных от центра. Диаметр - это отрезок, соединяющий любые две точки окружности через ее центр. Таким образом, окружность - это кривая, а диаметр - это отрезок.
Какая взаимосвязь между окружностью и диаметром?
Диаметр окружности является наибольшим из всех возможных отрезков, соединяющих две точки окружности через ее центр. Значит, диаметр делит окружность на две равные части. В то же время, любой диаметр можно рассматривать как частный случай окружности с бесконечным радиусом.
Может ли диаметр окружности быть равен ее радиусу?
Диаметр окружности равен удвоенному радиусу, так как диаметр проходит через центр окружности и состоит из двух радиусов. Если диаметр равен радиусу, то это будет случай, когда диаметр совпадает с самой окружностью, то есть окружность будет иметь нулевой радиус.



