Среднее квадратичное отклонение (стандартное отклонение) является одним из основных показателей разброса данных в статистике. Оно представляет собой меру разброса случайной величины относительно её среднего значения. Величина среднеквадратичного отклонения позволяет оценивать степень различия между значениями ряда и его средним.
Применение среднего квадратичного отклонения в статистике широко используется для анализа данных и принятия решений. Оно позволяет определить степень разброса данных, их надёжность и предсказуемость. Стандартное отклонение является важным инструментом при проведении статистических исследований, а также в финансовой аналитике и бизнесе.
Значение статистического показателя

Определение и основные принципы

Основными принципами расчета среднего квадратичного отклонения являются следующие шаги:
| 1. | Вычислить среднее значение выборки. |
| 2. | Для каждого значения выборки вычислить квадрат разности между ним и средним значением. |
| 3. | Найти сумму всех квадратов разностей. |
| 4. | Полученную сумму разделить на количество значений в выборке. |
| 5. | Извлечь квадратный корень из полученного значения, чтобы найти стандартное отклонение. |
Применение в анализе данных
- Оценка дисперсии: Среднее квадратичное отклонение используется для оценки дисперсии данных, т.е. для определения, насколько среднее значение отклоняется от каждого отдельного значения в наборе данных.
- Оценка надежности измерений: Стандартное отклонение помогает оценить точность и надежность измерений путем определения степени вариации данных.
- Сравнение наборов данных: Среднее квадратичное отклонение также используется для сравнения различных наборов данных и определения их степени разброса.
Различные сферы использования

Среднее квадратичное отклонение широко применяется в различных областях, включая:
- Физика: для измерения погрешности экспериментальных данных;
- Финансы: для оценки риска инвестиций;
- Инженерия: для анализа качества производства и технических характеристик;
- Медицина: для изучения различий в показателях здоровья и лечения;
- Социология: для анализа данных общественных опросов и исследований.
Среднее квадратичное отклонение является важным инструментом статистического анализа и помогает оценить разброс данных и их дисперсию в различных областях деятельности.
Расчет и интерпретация

Среднее квадратичное отклонение вычисляется путем нахождения квадратного корня из дисперсии. Для этого необходимо вычесть каждое значение в выборке на среднее арифметическое, возвести полученные разности в квадрат, сложить их, поделить на количество элементов выборки и извлечь корень.
Среднее квадратичное отклонение позволяет оценить разброс значений в выборке относительно среднего. Чем больше это значение, тем больше вариация данных. Если среднее квадратичное отклонение близко к нулю, то значения в выборке сконцентрированы вокруг среднего, а если оно большое, то данные имеют большой разброс.
Методы вычисления среднего квадратичного отклонения
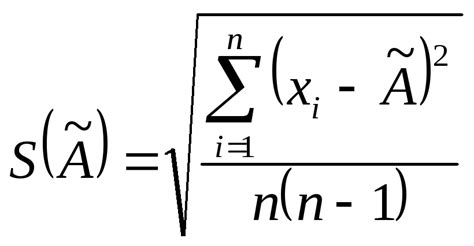
Существует несколько методов вычисления среднего квадратичного отклонения:
- Метод разности: вычисление отклонения каждого значения от среднего, их возведение в квадрат, суммирование и деление на количество значений.
- Метод квадратов: суммирование квадратов значений, вычитание квадрата среднего и деление на количество значений.
- Метод корня: вычисление среднего арифметического квадратов значений и извлечение квадратного корня.
Выбор метода зависит от конкретной задачи и предпочтений исследователя.
Значимость среднего квадратичного отклонения в статистике

Вопрос-ответ

Зачем нужно среднее квадратичное отклонение в статистике?
Среднее квадратичное отклонение является мерой разброса данных относительно их среднего значения. Оно позволяет оценить степень изменчивости данных и определить, насколько они распределены вокруг среднего. Эта характеристика позволяет делать выводы о точности и надежности данных в выборке.
Как вычисляется среднее квадратичное отклонение?
Для вычисления среднего квадратичного отклонения необходимо выполнить несколько шагов. Во-первых, нужно найти разность между каждым значением и средним арифметическим значением выборки. Затем эти разности нужно возвести в квадрат, сложить, поделить на количество элементов в выборке и извлечь корень из этой суммы. Формула: S = sqrt((Σ(xi - x̄)²) / N).



