Доказательство – это процесс, который подтверждает истинность теоремы. В ходе доказательства используются аксиомы, определения и ранее доказанные теоремы. Доказательства строятся логически последовательно и позволяют убедиться в правильности математических утверждений.
Доказательства теорем играют ключевую роль в развитии математики и позволяют строить новые математические теории. В статье рассмотрим несколько примеров теорем и их доказательств, чтобы проиллюстрировать процесс математического рассуждения.
Теорема - основной элемент математики
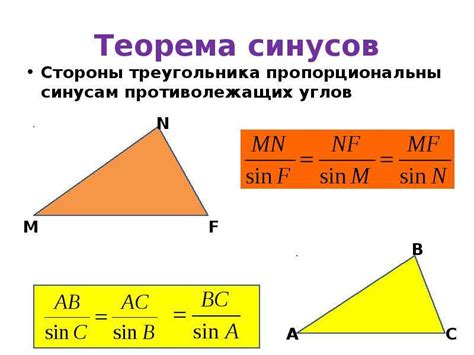
Основные компоненты теоремы - это гипотеза (предположение) и утверждение (что следует из гипотезы). Доказательство теоремы должно быть строгим, логичным и верным, чтобы убедить в правильности утверждения.
Примерами известных теорем являются теорема Пифагора, теорема Ферма, теорема о существовании и единственности решения и другие. Теоремы играют важную роль в образовании математиков и исследовании новых математических концепций и закономерностей.
Смысл и значение
Теорема в математике представляет собой утверждение, которое может быть доказано с использованием логических рассуждений на основе определенных аксиом или принятых гипотез. Доказательство теоремы представляет собой последовательность логических шагов, которые подтверждают истинность утверждения. Теоремы играют ключевую роль в математике, поскольку они развивают наше понимание аксиоматических систем и открывают новые связи между математическими понятиями.
Таким образом, понимание смысла и значения теорем в математике открывает для нас новые горизонты познания и позволяет использовать математические методы для решения разнообразных задач в различных областях научного знания.
Примеры из различных областей

2. В алгебре: Доказательство теоремы о средних пропорционалах - если a/b = c/d, то a+c/b+d = a/b = c/d.
3. В теории вероятностей: Доказательство формулы Бернулли - рассчитывается вероятность того, что в серии независимых испытаний количество успехов совпадает с заданным числом.
4. В теории чисел: Доказательство теоремы Ферма - знаменитая гипотеза была доказана для n=3.
5. В математическом анализе: Доказательство теоремы Вейерштрасса - для любой непрерывной функции на отрезке существует точка, в которой достигается максимальное и минимальное значение.
Доказательство - ключевая часть математики

Важными элементами доказательства являются логическая стройность, четкость и строгость аргументации. Доказательство должно быть составлено таким образом, чтобы его можно было легко проверить и однозначно определить его правильность.
Процесс доказательства требует от математика тщательности, логического мышления и способности выражать свои мысли четко и лаконично. Доказательство - это не просто набор формальных шагов, но и процесс, который позволяет обосновать математическую истину.
Доказательство существования

Доказательство существования играет важную роль в математике, поскольку позволяет утверждать, что искомый объект действительно существует. Это изучение существования решения уравнений, существования определенного объекта или структуры в математической теории или задаче.
Примером доказательства существования может быть с помощью конструкции или метода, приводящего к явному нахождению искомого объекта или при использовании теорем о существовании и единственности. Доказательство существования объекта важно для обоснования математических утверждений и решения задач.
Доказательство утверждения
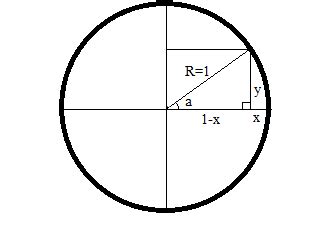
Основные методы доказательства включают индукцию, от противного, доказательство по определению, конструкции, и т.д. Каждый метод имеет свои особенности и применяется в зависимости от конкретной задачи.
Теорема и доказательство в математике: важность и применение
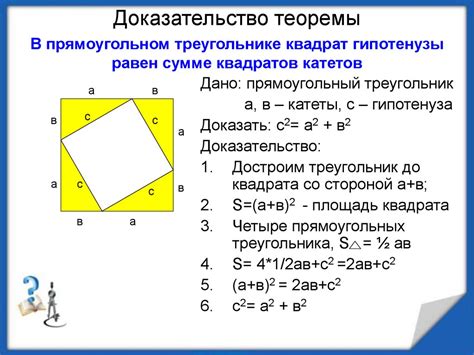
Теоремы и их доказательства играют ключевую роль в математике, помогая устанавливать законы и связи между математическими объектами. Они служат фундаментом для построения новых результатов и развития математической науки.
Важность теорем заключается в их способности формализовать и систематизировать знания, делая математику точной и объективной. Доказательства теорем позволяют убедиться в их истинности и логической стройности, что является основой для принятия новых математических утверждений.
Применение теорем и их доказательств в математике распространено почти во всех ее областях, от алгебры до геометрии, от анализа до теории вероятностей. Это позволяет математикам строить новые теории, разрабатывать методы и решать сложные задачи на основе уже установленных математических фактов.
Роль теоремы и доказательства в науке

Теоремы и их доказательства играют важную роль в научном познании. Они представляют собой стройную систему логических утверждений, которые выражают связь между различными понятиями в математике.
Доказательство теоремы – это логическое обоснование достоверности утверждения. Оно представляет собой серию логических шагов, строгих рассуждений и использование уже известных фактов.
Практическое применение в различных областях

В области информационных технологий теоремы часто применяются при проектировании вычислительных систем, криптографии, компьютерной графики и других областях.
В физике теоремы математики используются для моделирования физических процессов, анализа данных экспериментов и разработки новых теорий.
В экономике и финансах математические теоремы применяются при анализе рынков, прогнозировании и оптимизации финансовых потоков.
Таким образом, умение применять математические теоремы и их доказательства в различных областях позволяет исследователям и специалистам эффективно решать сложные задачи, создавать новые технологии и улучшать существующие процессы.
Вопрос-ответ

Что такое теорема в математике?
Теорема в математике - это утверждение, которое может быть доказано с использованием логических рассуждений и предыдущих математических знаний. Теорема обычно состоит из условия и вывода (следствия), и означает определенное свойство или закономерность в математике.
Можете привести пример теоремы в математике?
Пример теоремы в математике - теорема Пифагора, которая утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Это известное утверждение имеет условие (наличие прямого угла) и вывод (формула), и может быть доказано различными методами, например, геометрически или алгебраически.



