Материальные точки – это объекты, у которых масса сосредоточена в одной точке и не имеют пространственного размера. Изучение движения материальных точек является основой для понимания различных физических явлений и законов.
Траектория – это линия, по которой движется точка, принимая во внимание время и пространственные координаты. Интересное направление исследования – это случаи, когда траектории не только пересекаются, но и взаимодействуют друг с другом.
В данной статье мы проведем анализ траекторий пересекающихся материальных точек с использованием различных методов математического моделирования и физических законов. Узнаем, как взаимодействие точек может изменять направление и форму их движения, а также какие закономерности можно обнаружить в таких системах.
Исследование траекторий
Для анализа траекторий используются математические методы, такие как дифференциальные уравнения и параметризация кривых. С помощью этих методов можно определить форму и характер движения точек, а также выявить особенности и закономерности их траекторий.
Исследование траекторий пересекающихся материальных точек позволяет предсказать и описать поведение системы точек в различных условиях. Это помогает улучшить понимание процессов, происходящих в системе, и использовать полученные данные для решения различных практических задач.
Пересекающиеся точки
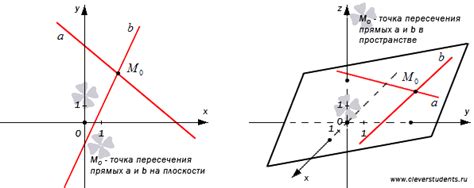
Изучение траекторий пересекающихся материальных точек позволяет анализировать их взаимодействие и влияние друг на друга. Важно учитывать параметры движения каждой точки, а также точки их пересечения. Это позволяет предсказывать последующие траектории и состояние системы в целом. При изучении пересекающихся точек необходимо учитывать их скорости, ускорения и массы, так как это оказывает существенное влияние на динамику системы.
| Точка | Скорость | Ускорение |
|---|---|---|
| Точка A | 10 м/с | 2 м/с² |
| Точка B | 8 м/с | 3 м/с² |
Материальных объектов

Материальные объекты могут быть твердыми, жидкими или газообразными, и каждый из них обладает своими уникальными свойствами. Исследование их движения и взаимодействия является основой для понимания физических явлений и является ключевым элементом в научных исследованиях.
- Твердые материальные объекты имеют определенную форму и объем, и сохраняют свою структуру при воздействии внешних сил.
- Жидкие материальные объекты имеют определенный объем, но не сохраняют форму и принимают форму сосуда, в котором они находятся.
- Газообразные материальные объекты не имеют определенной формы и объема, а распространяются по всему доступному пространству.
Изучение материальных объектов и их свойств позволяет углубить наши знания о механике, термодинамике, оптике и других разделах физики, а также применять эти знания для практических целей, например, в инженерии, медицине и промышленности.
Движение в пространстве
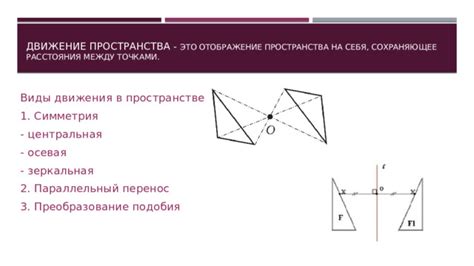
Для анализа движения системы точек в пространстве часто используются векторы положения, скорости и ускорения. Вектор скорости материальной точки представляет собой производную от вектора положения по времени, а вектор ускорения - производную от вектора скорости.
При изучении движения пересекающихся материальных точек важно учитывать их траектории и взаимодействия. Анализ траекторий позволяет предсказать перемещение точек в пространстве и выявить закономерности в их поведении.
| Траектория | Описание |
|---|---|
| Прямолинейное движение | Точки движутся по прямой линии без изменения направления. |
| Криволинейное движение | Точки движутся по кривой линии, изменяя направление движения. |
| Вращательное движение | Точки вращаются вокруг оси, сохраняя определенное расстояние до нее. |
Вопрос-ответ

В чем заключается основная цель исследования траекторий пересекающихся материальных точек?
Основная цель исследования траекторий пересекающихся материальных точек заключается в определении взаимодействия и движения данных точек в пространстве. Это позволяет лучше понять кинематику системы материальных точек и предсказывать их поведение в различных условиях.
Какие методы используются для анализа траекторий пересекающихся материальных точек?
Для анализа траекторий пересекающихся материальных точек часто применяются методы математической физики и динамики. Это включает в себя использование уравнений движения, анализ энергии системы, применение законов сохранения и численные методы моделирования.
В чем заключается практическая значимость исследования траекторий пересекающихся материальных точек?
Практическая значимость исследования траекторий пересекающихся материальных точек проявляется во многих областях, таких как аэрокосмическая индустрия, механика, физика и другие. Это позволяет разрабатывать более точные модели движения объектов, улучшать прогнозирование поведения систем и оптимизировать проектирование различных устройств.



