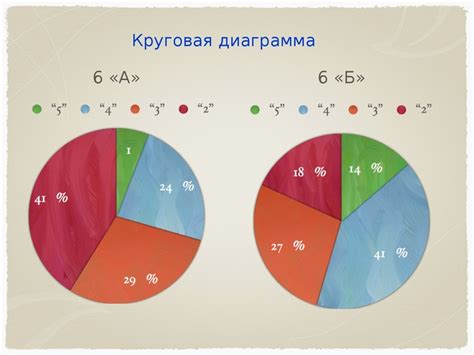
Точность – одно из ключевых понятий при построении круговых диаграмм для анализа данных. Правильное отображение информации в диаграмме является основой для корректного толкования результатов и принятия обоснованных решений.
Недостаточная точность при построении секторов круговой диаграммы может искажать представление о данных и вводить в заблуждение. Поэтому важно уделить внимание правильному расчету и отображению секторов для достоверного анализа информации.
Роль точности в анализе данных

Точность в анализе данных означает правильность и достоверность информации. При построении диаграмм точность определяет правильное распределение данных по секторам, что в свою очередь влияет на правильное толкование результатов анализа.
Необходимо помнить, что недостаточная точность может исказить истинное положение вещей, в то время как достоверные данные помогут увидеть реальную картину и принимать обоснованные решения. Поэтому важно придавать значение точности при анализе и визуализации данных.
Значение точности для круговых диаграмм
Методы улучшения точности
1. Выбор правильного количества секторов: оптимальное количество секторов в круговой диаграмме поможет избежать избыточной детализации и сделает данные более понятными для анализа.
2. Использование подписей и легенды: четкие подписи секторов и наглядная легенда сделают диаграмму более информативной и позволят увереннее интерпретировать данные.
3. Представление процентного соотношения: добавление процентного значения к каждому сектору поможет визуально представить долю каждой категории и сравнивать их между собой.
Выбор подходящей метрики

Для выбора подходящей метрики необходимо учитывать цель и контекст анализа данных. Например, если основной интерес лежит в сравнении долей различных категорий, то следует выбрать пропорциональную метрику, такую как процент или доля. Если же важно отразить абсолютные значения, то лучше использовать числовую метрику.
Необходимо помнить, что точность выбора метрики существенно влияет на интерпретацию данных и принимаемые решения. Поэтому перед построением круговой диаграммы необходимо тщательно обдумать и выбрать подходящую метрику для каждого сектора.
| Цель анализа | Подходящая метрика |
|---|---|
| Сравнение долей | Процент, доля |
| Отражение абсолютных значений | Числовая метрика |
Оптимальный угол секторов
Слишком маленькие углы делают секторы едва заметными, в то время как слишком большие углы могут привести к перегруженному и сложному для восприятия графику. Оптимальный угол обычно лежит в диапазоне от 20 до 60 градусов, в зависимости от количества данных и их значимости.
Влияние точности на интерпретацию
Если данные не точны или содержат ошибки, то круговая диаграмма может искажать реальное положение вещей. Например, если значение какой-то категории недооценено или завышено из-за неточности данных, то это может привести к неверному искажённому восприятию.
Поэтому важно предоставлять только точные данные для построения круговых диаграмм и дополнительно проверять их на достоверность перед анализом и интерпретацией.
Ошибки из-за низкой точности
Примеры успешного анализа данных

Дополнительный пример:
Анализ доходов компании по разным видам услуг также успешно проводится с помощью круговых диаграмм. Это помогает идентифицировать наиболее и наименее прибыльные виды услуг и принять решения о дальнейшей стратегии развития бизнеса.
Вопрос-ответ

Почему так важно правильно определять углы секторов круговой диаграммы?
Точное определение углов секторов круговой диаграммы имеет ключевое значение, поскольку именно от этого зависит правильное представление данных. Неправильно построенные сектора могут ввести в заблуждение и исказить восприятие информации. Корректные углы позволяют корректно сравнить доли различных категорий данных и делать точные аналитические выводы.
Как определить точность углов секторов круговой диаграммы?
Для определения точности углов секторов круговой диаграммы важно использовать правильный метод расчета. Необходимо корректно вычислить долю каждой категории данных от общего объема и преобразовать ее в угловое значение, учитывая, что полный круг равен 360 градусам. Также важно правильно расположить секторы относительно центра диаграммы, чтобы избежать искажений при визуализации результатов.



