Векторы являются важным понятием в линейной алгебре и математике в целом. Они играют значительную роль и в геометрии, в том числе в изучении треугольников. В данной статье мы рассмотрим свойства векторов в треугольнике, включая коллинеарность, направление, их взаимное расположение и другие характеристики.
Коллинеарность векторов в треугольнике означает, что они лежат на одной прямой. Это важное свойство, которое позволяет нам рассматривать векторы как элементы взаимосвязи точек треугольника. Понимание коллинеарности векторов позволяет углубить знания о геометрии и связанных с ней математических концепциях.
Векторы в треугольнике
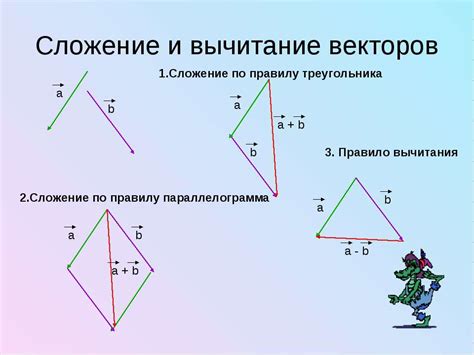
Векторы играют важную роль при изучении свойств треугольников. Векторы обладают такими свойствами, как коллинеарность и направление. Коллинеарные векторы лежат на одной прямой, а направление вектора задается его направлением и длиной.
Для треугольника ABC с вершинами A, B и C стороны треугольника и его диагонали могут быть представлены векторами. Так, вектор AB будет равен вектору BC минус вектору AC: AB = BC - AC. Для проверки коллинеарности векторов в треугольнике, можно применить правило, что векторная сумма сторон треугольника равна нулевому вектору: AB + BC + CA = 0.
Примером использования векторов в треугольнике может быть нахождение площади треугольника по векторному произведению его сторон. Векторное произведение двух сторон треугольника равно половине длины его площади.
Коллинеарность векторов

Для проверки коллинеарности векторов нужно убедиться, что они либо параллельны, либо отличаются только по длине, в случае если они лежат на одной прямой.
Коллинеарные векторы имеют различные свойства, такие как равенство направления, кратные отношения длин, равномерное смещение. Это свойство важно при решении задач, связанных с линейной алгеброй и геометрией.
Свойства векторов в треугольнике
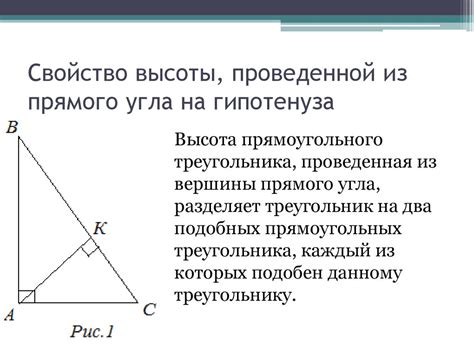
В треугольнике вершины образуют замкнутую фигуру, поэтому сумма векторов, соединяющих вершины треугольника, равна нулевому вектору. Это свойство называется замкнутостью системы векторов.
Также вектор, соединяющий середины двух сторон треугольника параллелен и равен половине третьего вектора. Это свойство называется параллельностью и равенством векторов.
Основное свойство векторов в треугольнике - коллинеарность. То есть векторы, соединяющие вершины треугольника, коллинеарны, если соответствующие стороны треугольника параллельны. Это свойство позволяет упрощать вычисления и находить различные зависимости между векторами в треугольнике.
Сложение векторов в треугольнике
| Свойство | Формула |
|---|---|
| Закон параллелограмма | Если два вектора a и b соединены концами, то их сумма равна вектору c, который является диагональю параллелограмма, образованного векторами a и b. |
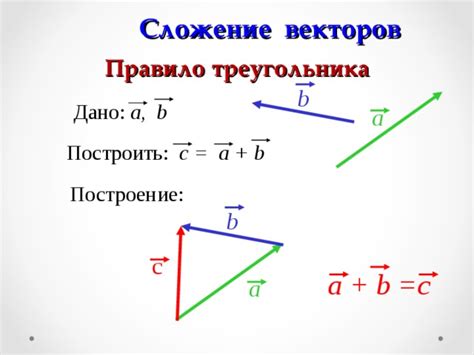
| Закон треугольника | Для треугольника ABC сумма двух векторов, направленных по сторонам треугольника, равна вектору, проведенному от одного угла треугольника до середины противолежащей стороны. |
| Пример | Пусть вектора a и b направлены вдоль сторон AB и AC треугольника ABC соответственно. Сумма этих векторов совпадает с вектором, проведенным от вершины A треугольника до середины BC. |
Разложение векторов в треугольнике
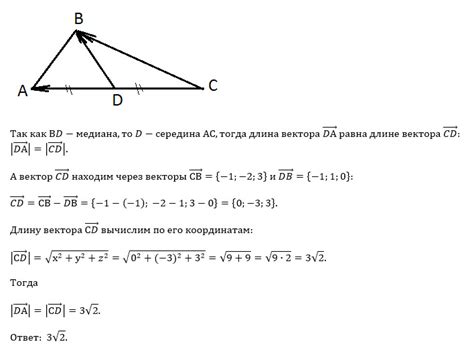
Итак, предположим, что у нас есть треугольник ABC, и известны векторы AB (a) и AC (b). Нам нужно найти вектор BC (c), принадлежащий стороне треугольника. Для этого мы можем воспользоваться равенством треугольников: BC = AB - AC = a - b.
Таким образом, разложение вектора BC на векторы AB и AC дает нам возможность эффективно находить новые векторы в треугольнике, используя известные векторы сторон.
Примеры использования векторов в треугольнике

Векторы широко используются при решении задач, связанных с треугольниками. Например, для нахождения площади треугольника можно использовать векторное произведение двух его сторон.
Пример 1: Пусть дан треугольник ABC. Найдем площадь треугольника, зная координаты его вершин A(x1, y1), B(x2, y2), C(x3, y3). Пусть вектора AB = (x2 - x1, y2 - y1) и AC = (x3 - x1, y3 - y1). Тогда площадь треугольника ABC равна половине модуля векторного произведения этих векторов.
Пример 2: Также с помощью векторов можно проверить коллинеарность точек в треугольнике. Если точки A, B и C коллинеарны, то вектор BC будет коллинеарен вектору AB или AC. Это свойство можно использовать при изучении расположения точек в треугольнике.
Практическое применение векторов в треугольнике
Применение векторов в треугольнике важно для решения различных геометрических задач. С их помощью можно находить медианы, биссектрисы, высоты треугольника, а также находить углы, длины сторон и площадь фигуры.
Примеры практического применения векторов в треугольнике:
1. Нахождение площади треугольника по координатам вершин с помощью векторного произведения.
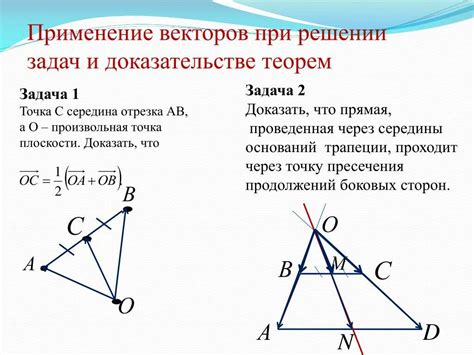
2. Поиск точки пересечения медиан треугольника с использованием метода векторов.
3. Решение задач на построение треугольника и нахождение его элементов по заданным условиям, например, равнобедренности или подобия.
Использование векторов в геометрии дает возможность работать с треугольниками более эффективно и точно, облегчая решение сложных задач.
Особенности расчетов с векторами в треугольнике
При работе с векторами в треугольнике важно помнить о следующих особенностях:
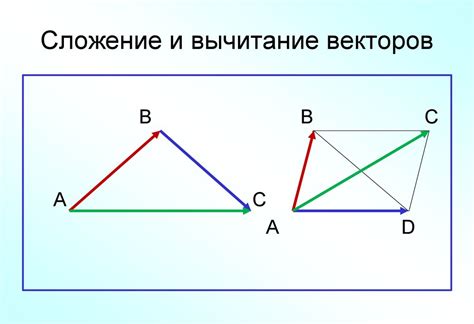
- Для нахождения суммы векторов в треугольнике используется правило параллелограмма: сумма двух векторов равна вектору, который является диагональю построенного параллелограмма.
- Для нахождения разности векторов в треугольнике можно использовать ту же концепцию - построить параллелограмм и взять вектор, соединяющий начало первого вектора с концом второго.
- Векторное произведение двух векторов в треугольнике равно площади параллелограмма, образованного этими векторами.
Вопрос-ответ

Что такое коллинеарные векторы в треугольнике?
Коллинеарные векторы в треугольнике - это векторы, лежащие на одной прямой или параллельные друг другу. В треугольнике коллинеарные векторы могут быть направлены внутри треугольника или за его пределы.
Какую роль играют векторы в треугольнике?
Векторы в треугольнике используются для описания смещений и направлений отрезков между точками треугольника, а также для решения задач на равенство трех подобных треугольников.
Какие свойства имеют коллинеарные векторы в треугольнике?
Коллинеарные векторы в треугольнике имеют одинаковые или противоположные направления, и их линейная комбинация может быть выражена через коэффициенты пропорциональности. Кроме того, коллинеарные векторы обладают свойством равенства их длин.
Как можно использовать коллинеарные векторы в треугольнике на практике?
Коллинеарные векторы в треугольнике могут быть использованы для доказательства существования точки пересечения медиан треугольника, для вычисления площади треугольника по длинам его сторон и других задач с использованием векторов и их свойств.



